4.1 Превосходство портфелей, состоящих из акций и опционов колл
Здесь мы покажем, как инвестиция в опционы может превзойти инвестицию в акции при любом рынке: и при подъеме, и при падении. Мы покажем, что это возможно благодаря использованию специфически изогнутой линии цены. Для этого мы рассмотрим еще раз одногодичный опцион колл, показанный на Рисунке 3.7. Вспомните, что один опционный контракт может быть исполнен на 100 акций, но его экспозиция по акции изменчива и зависит от цены базового инструмента.
Мы собираемся сравнить две ситуации, в которых находятся менеджеры фондов, располагающие 50 акциями какой-либо компании. Цена рассматриваемой акции $99,00, а одногодичный опцион колл оценивается в $5,46. Один менеджер фонда имеет длинную позицию на 50 акций, а другой обладает длинной позицией на одногодичный опцион колл. Из обсуждений в третьей главе мы поняли, что менеджер фонда, владеющий опционом, находится в точке "В", как это было представлено на Рисунке 3.7, где дельта равна 0,50, а экспозиция по акции равна 50 бумагам. На языке опционного рынка можно сказать, что оба портфеля дельта-эквивалентны (delta equivalent).
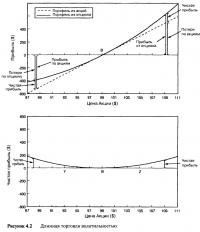
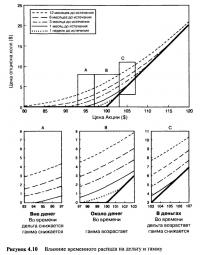
Хотя экспозиция по акции у каждого из менеджеров одинакова, реальные стоимости портфелей разные. Менеджеру, который инвестировал в акции, потребовался капитал в 50x99=$4.550, в то время как менеджер, инвестировавший в опцион, вложил 100x5,46=$546. Поскольку нас интересует только то, что происходит с обоими менеджерами в момент создания портфелей, то мы "подведем к нулю" портфели, убрав первоначальные величины инвестиций. Соответственно, мы вычитаем $4.550 и $546 из стоимостей портфелей, которые наблюдаются при последующих ценах акций. Таблица 4.1 и Рисунок 4.1 дают представление о том, что происходит, если цена акции, лежащей в основе портфелей менеджеров, отклоняется от начальной стоимости в $99 в сторону уменьшения или увеличения.
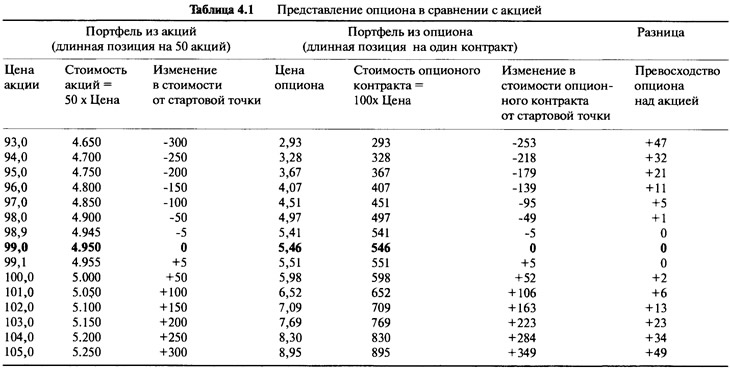
Мы видим, что при очень маленьких изменениях цены акции оба портфеля ведут себя почти одинаково. Этого и следовало ожидать. Мы специально взяли такое количество ценных бумаг для портфеля, который включает в себя только акции, чтобы экспозиция была сходна с портфелем, состоящим из опциона. Мы намеренно выбрали такой наклон линии прибылей и убытков портфеля из акций, чтобы он в точности совпал с наклоном опционного портфеля в точке "В". Однако когда мы начнем рассматривать большие ценовые движения акции, ситуация изменится.
Увеличение цены акции
Если цена акции увеличивается с $99 до $101, стоимость портфеля, состоящего только из акции, увеличивается на $100. В соответствии с этим стоимость опциона увеличивается с $5,46 до $6,52, что приводит к увеличению стоимости контракта на $106. Это демонстрирует превосходство портфеля опциона в $6 над портфелем из акции. Если цена акции поднимется еще выше, то относительное превосходство станет более заметным. При цене в $105 превосходство возрастет до $49.
Уменьшение цены акции
Если цена акции падает с $99 до $97, то стоимость портфеля, состоящего из акций, уменьшается на $100. Цена опциона соответствующим образом уменьшается с $5,46 до $4,51, что приводит к снижению стоимости контракта на $95. При падающем рынке опционный портфель теряет стоимость, но в меньшей степени, чем портфель из акций. Таким образом, по-прежнему можно говорить о превосходстве портфеля из опциона в $5 над портфелем из акций. Если цена акции упадет еще ниже, то относительное превосходство станет более заметным. При цене акции в $93 превосходство вырастет до $47.
Итак, получается, что менеджер, инвестирующий в опцион, "превосходит" менеджера, инвестирующего в акции, если цена акции падает или растет (rises orfalls), а почему так происходит, объясняется на Рисунке 4.1. Стоимость опциона изгибается над прямой линией, отражающей стоимость акции, по обе стороны от точки "В". Причины, по которым это происходит, мы разобрали в третьей главе. Этот пример может показаться сложным из-за того, что цифры были выбраны таким образом, чтобы исходные экспозиции по акции были одинаковы, но всегда можно увидеть, что опционный портфель совпадает с первоначальными экспозициями. А из-за того, что профиль стоимости опциона искривлен, преимущества, о которых говорилось выше, будут достижимы всегда. Тогда ради чего вообще нужно связываться с акциями? Почему бы всегда не использовать опционы? Использование опционов, конечно же, не гарантирует получение прибыли, но, по крайней мере, имеет преимущество по сравнению с использованием акций. Однако дело в том, что мы объяснили далеко не все. Есть одна ловушка (catch). Это вторая сторона вопроса, которую мы обсудим позже.
Между тем было бы более правильным сказать, что портфель, состоящий из опциона колл, будет явно превосходить в дельта-эквиваленте портфель, состоящий из акций, в вышеуказанном примере, если произойдут значительные ценовые изменения.
4.2 Дельта нейтральная торговля длинной позицией по волатильности
Теперь мы подробно рассмотрим механизм покупки волатильности. Предположим, что в обозримом будущем цена интересующей нас акции будет сильно колебаться. Допустим, мы точно знаем: как бы ни колебалась цена, ее изменения будут значительными и таких ценовых движений будет много. К сожалению, мы не знаем, в каком направлении будет двигаться цена и когда это направление изменится. Конечно, незнание направления развития цены будет серьезным пробелом. Нам придется создать такое положение, при котором прибыль будет получена при любом направлении развития цены: как вверх, так и вниз. Эта задача может показаться трудной, но решить ее возможно. Нам нужно начать с позиции, которая первоначально рыночно-нейтральна, но которая становится длинной, если рынок поднимается, и короткой, если рынок падает.
Если мы посмотрим на Таблицу 4.1 и Рисунок 4.1, где сравниваются ситуации с участием двух менеджеров, то получим ответ. Оба менеджера фондов первоначально должны иметь длинную позицию на то же самое количество акций или быть в такой позиции, в которой при малых изменениях имеются одинаковые изменения в сторону прибылей и убытков. К сожалению, в этом примере оба менеджера обладают длинной позицией, поэтому могут заработать прибыль только при подъеме рынка. Мы же хотим, чтобы в любом случае сначала у нас была бы рыночно-нейтральная конструкция.
Решение заключается в том, чтобы иметь портфель, состоящий из длинной позиции на один опционный контракт и одновременно короткой позиции на 50 акций. Иными словами, должна быть длинная позиция опционного менеджера и короткая позиция менеджера акциями. Таким образом, экспозиции по акциям обоих компонентов становятся одинаковыми, но с противоположными знаками, а следовательно должны уравновешиваться. Мы будем называть это портфелем, состоящим из длинной позиции по волатильности, или хеджированным портфелем. Вычисление изменения стоимости этого портфеля совсем простое. Мы просто перевернем знаки стоимости портфеля из акций, обратившись к данным в Таблице 4.1. Результирующий вид портфеля, сконструированного как длинная волатильная позиция, отражен в Таблице 4.2 и на Рисунке 4.2.
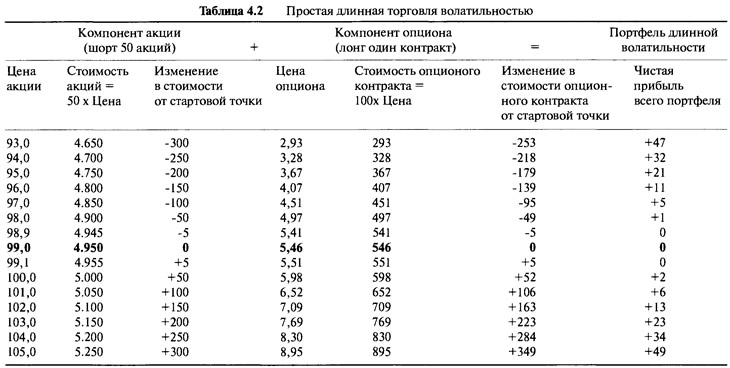
При растущем рынке прибыль менеджера акциями становится убытком, и этот убыток должен быть вычтен из опционной прибыли. На падающем рынке потери менеджера акциями становятся прибылью, и эта прибыль должна быть добавлена к убыткам от опционов. На Рисунке 4.2 мы видим кривую прибылей и убытков акции как позитивно наклоненную линию, но на самом деле она отрицательна. Все на том же Рисунке можно легко увидеть, что чистая прибыль хеджированного портфеля становится разницей между двумя линиями стоимости, и это показано отдельно на нижнем графике. Чистая прибыль является просто измерением того превосходства, которое было показано в Таблице 4.1.
Малые ценовые движения акции
Если подъем цены акции небольшой, то опционная прибыль почти полностью уравновешивается убытком от короткой позиции на акцию. Поэтому при малых ценовых движениях вверх или вниз результатов в виде прибыли или убытка не наблюдается. Позиция полностью хеджирована. Владелец такой позиции называется рыночно-нейтральным, или дельта-нейтральным. Это как если бы держатель акции вообще не принимал никакого участия в рынке.
Суть этой позиции — в правильном сочетании акции и опциона. Соотношение здесь составляет 0,5 — это и есть дельта. Любая другая пропорция между акцией и опционом не будет рыночно-нейтральной. Читатель может выполнить небольшое упражнение: попробовать разные соотношения и доказать, что убытки и прибыль возникают при малых ценовых движениях. Поскольку пропорция так важна при создании хеджированного портфеля, то дельту часто называют коэффициентом хеджа (hedge ratio).
Большие ценовые движения акции
Если цена акции значительно поднимается, тогда опционный компонент создает больше, чем теряется со стороны акции. Если цена акции значительно падает, тогда прибыль от короткой позиции на акцию всегда превышает потери от опционного компонента. Чем больше движение вверх или вниз, тем больше прибыль. Создав эту позицию, мы будем надеяться на большие рыночные движения, поэтому эта стратегия называется длинной торговлей волатильностью.
Итак, в каком бы направлении ни происходило движение акции, мы всегда получаем прибыль. В этом суть длинной торговли волатильностью.
На Рисунке 4.2 графически показано, что торговля является производительной просто из-за наличия ценового изгиба. Также заметьте, что результирующий профиль прибылей тоже изогнут. Крайне полезно рассмотреть стратегию с точки зрения экспозиции по акции. Начнем с точки "В", где обе позиции имеют равные, но противоположные экспозиции, то есть начинаем с рыночно-нейтрального положения. Если цена базовой акции растет, то экспозиция опциона по акции поднимается над постоянной экспозицией короткой позиции на акцию, поэтому весь портфель автоматически становится длинным. Чем значительней движение, тем более портфель становится лонг. И наоборот, если цена лежащей в основе стратегии акции падает, то экспозиция опциона опускается ниже постоянной экспозиции короткой позиции на акцию, поэтому весь портфель автоматически становится коротким. Чем значительней движение, тем более портфель шорт. Это — в идеальном случае. Мы автоматически оказываемся в длинной позиции, если рынок растет, и в короткой, если рынок падает.
Ничего не предпринимать, находясь в длинной торговле волатильностью
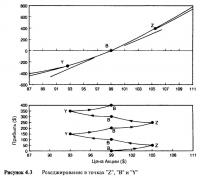
Что произойдет, если мы войдем в торговлю в точке "В" и нам посчастливится стать свидетелями резкого подъема цены акции до $105, или точки "Z"? Мы запишем прибыль в $49, но на данный момент эта прибыль находится лишь на бумаге и еще не выручена. Что будет, если мы понадеемся на то, что нам повезет, и цена акции продолжит свой рост? Если цена действительно будет расти, тогда мы, конечно, получим большую прибыль, но что произойдет, если цена акции будет все время падать на протяжении всего пути до точки "В"? Прибыль исчезнет. Нам может опять повезти, если цена будет продолжать падать до $93, или до точки "V, в которой мы сможем опять записать прибыль, на этот раз в $47. Если такое случится и мы все еще ничего не предпринимаем, тогда цена может снова вырасти до точки "В", что опять не принесет прибыли. Если мы не будем действовать, то, скорее всего, нам придется фиксировать на бумаге прибыль, а затем наблюдать ее исчезновение, затем снова фиксировать прибыль и так далее. Как нам фиксировать прибыль, возникающую из наличия волатильности?
Рехеджирование длинной позиции по волатильности
Давайте вернемся к первоначальной отметке: торговле в точке "В". Если первое значительное движение вверх составляет $6 — до $105 в точке "Z", тогда мы имеем первую отметку на бумаге о прибыли в $49. Простейший способ зафиксировать эту прибыль это полностью ее ликвидировать (completely liquidate). Продать опцион по $8,95 и закрыть короткую позицию на акцию по $105, выйдя из торговли, удержав тем самым прибыль (небольшую) в $49.
Однако стратегия ликвидации не имеет особого смысла. Можно получить намного большую прибыль, не покидая позиций. Посмотрим на другого участника рынка, намеревающегося войти в эту стратегию в точке "Z". Он надеется, что рынок останется волатильным, и хочет извлечь выгоду из ценового изгиба опциона. Вопрос в том, какую пропорцию между акцией и опционом колл следует выбрать в точке "Z"? В точке "Z" дельта выше, она достигла величины в 0,66. Новому участнику нужно купить один опцион колл (обеспечивающий исполнение на 100 акций) и коротко продать 66 акций. Точно так же, как и в ситуации с первым участником, если рынок значительно растет или падает, то в результате получается прибыль.
Тогда почему же наш первый инвестор не вошел еще раз в рынок в точке "Z" с новыми соотношениями? Он мог бы, но зачем вообще выходить из торга? В реальной рыночной ситуации каждое действие стоит денег, и вместо того чтобы ликвидировать позиции и входить в них заново, почему бы не подобрать пропорцию между акциями и опционом? В точке "В" первый инвестор имел длинную позицию на один опцион колл и короткую на 50 акций. В точке "Z", чтобы быть строго рыночно-нейтральным, сочетание должно состоять из длинной позиции на один опцион колл и короткой на 66 акций. Проще всего будет продать дополнительно 16 акций (по цене $105), чтобы в итоге получилось 66. Теперь у инвестора правильное соотношение опциона и акций, а в результате ситуация опять дельта-нейтральная. В процессе рехеджирования (rehedging) примечательно то, что маленькая прибыль в $49 теперь зафиксирована, а инвестор возвращается обратно в круг деловых операций и продолжает ждать значительных движений вверх или вниз.
Откуда возникает прибыль в длинной торговле волатильностью?
Для того чтобы показать, что рехеджирование фиксирует прибыль, рассмотрим ситуацию, в которой цена акции снова падает до $99, то есть возвращается на точку "В". В точке "В" дельта снова становится 0,50, поэтому портфель здесь может иметь короткую позицию только на 50 акций. Портфель здесь слишком шорт, и соответственно, чтобы его рехед-жировать, мы просто купим обратно 16 акций по $99, переустановив позицию в новую, рыночно-нейтральную. Эта новая рыночно-нейтральная позиция, состоящая из длинной позиции на один опцион колл по $5,46 и короткой позиции на 50 акций по $99, идентична ситуации, с которой мы начали. Единственное различие состоит в том, что на пути от точки "В" до точки "Z" и обратно, все, что мы действительно сделали, — это продали 16 акций по $105, а потом купили их обратно по $99, получив прибыль 16 х (105-99) = $96. Эти $96 в действительности состоят из $49, заработанных на пути от "В" до "Z" и $47, заработанных на пути от "Z" до "В". Если бы мы ничего не предприняли в точке "Z" и не произвели рехеджирования, то прибыли никакой не было бы. Процесс рехеджирования фиксирует первоначальную прибыль и устанавливает положение, при котором она может быть получена в дальнейшем.
В идеале нам хотелось бы, чтобы цена акции неограниченно колебалась между точками "В" и "Z". Каждый цикл колебания принес бы нам прибыль в $96. Но такое вряд ли возможно. Давайте рассмотрим альтернативный сценарий падения цены акции от точки "Z" к точке "В", только на этот раз цена акции продолжает падать до точки "Y" — до $93. Помните, что сразу же после точки "В" мы рехеджируем, покупая обратно 16 акций, фиксируя общую прибыль в $96, переустанавливая здесь 50% пропорцию хеджа. При цене, падающей до точки "Y", опцион имеет новую, меньшую дельту, составляющую 0,34, поэтому количество акций в шорт может равняться только 34. Соответственно, мы рехеджируем, выкупая обратно 16 из тех 50 коротких акций по $93. Наконец, давайте представим, что цена акции движется обратно к точке "В". В точке "В", чтобы снова добиться нейтральной позиции, мы должны продать 16 акций (по $99), зафиксировав здесь вновь возникшую прибыль в 16х(99-93)=$96, в результате чего общая прибыль составила $192. Рисунок 4.3 показывает, как благодаря стратегии рехеджирования прибыль постепенно суммируется, если цена акции продолжает двигаться от "В" к "Z", потом к "В", далее "Y", к "В", и т.д.
В верхнем графике на Рисунке 4.3 проведены три разные касательные к кривой в точках "Y", "В" и "Z". Наклоны трех касательных представляют собой три разные дельты, а именно: 0,34, 0,50 и 0,66 соответственно. По мере того, как цена акции движется от одной точки к другой, пропорция между акцией и опционом приводится в соответствие с этими наклонами. Нижний график показывает чистую торговую прибыль. Начиная с точки "В" прибыль равна нулю. По мере продвижения цены акции от "В" до "Z" маленькая прибыль в $49 накапливается, что демонстрируется поведением кривой. В точке "Z" рехеджированная сделка переустанавливает дельта-нейтральную позицию. Затем цена движется обратно к точке "В". Обратный путь дает прибыль в $47, которая прибавляется к первоначальной прибыли в $49, что в итоге составляет $96. В точке "В" опять имеет место рехеджирование, и акция продолжает свой путь к точке "Y", принося дополнительную прибыль. На примере того, как цена акции продолжает двигаться туда и обратно, мы видим, как постепенно генерируется прибыль. В каждой точке рехеджирования скорость, с которой возникает прибыль, изменяется. Это потому, что в каждой точке рехеджирования устанавливается новая нейтральная позиция. Процесс постепенного рехеджирования, формирующий новые значения дельты позиции, называется динамическим хеджированием (dynamic hedging). Хотя пример достаточно сложный, он четко иллюстрирует то, как происходит торговля.
Несложно понять происхождение названия "длинная торговля волатильностью". Чем больше двигается цена акции, и чем чаще цена разворачивается, тем больше появляется возможностей для извлечения прибыли. Привлекательная сторона длинной торговли волатильностью состоит в том, что при рехеджировании инвестор вынужден продавать на поднимающемся рынке и покупать на падающем рынке. Торговля происходит в направлении, противоположном основной рыночной тенденции. Когда рынок быстро поднимается либо из-за какого-нибудь спекулятивного всплеска, либо из-за того, что некоторые участники рынка попали в ловушку позиций шорт, инвестор продает. В ситуации краха рынка, когда все начинают панически продавать, вы становитесь покупателем. Находясь на противоположной стороне от основного рынка, вы получаете легкое исполнение своих ордеров.
Итак, откуда берется прибыль при такой торговле? Ответ — от рехеджирования. Процесс рехеджирования заставляет нас всегда находиться в позиции покупки на низком уровне и продажи на высоком уровне (buying low and selling high).
А что, если цена акции только продолжает расти?
Предположим, цена акции, вместо того, чтобы снова падать после достижения отметки $105, продолжает расти до $110, а затем до $115 и так далее. На $110 дельта уже 0,76, поэтому акции снова должны быть проданы, чтобы получилась общая короткая позиция на 76 акций. По мере роста цены дельта тоже продолжает расти, поэтому следует продавать все больше акций. Может появиться отметка (в этом случае $140), в которой дельта достигнет максимума, равного 1,0. В этой точке портфель будет состоять из одного опционного контракта и короткой позиции из 100 акций. В этой точке стоимость опциона будет увеличиваться в точном линейном соответствии с ростом стоимости акции (потерь по шорт), и никакая прибыль уже не появится. При такой высокой цене акции никакого изгиба в профиле опционной цены уже не будет. Важно заметить, что никто никогда не окажется в чисто короткой позиции. Никто не сможет открыть короткую позицию больше, чем на 100 акций. Продолжение рехеджирования зафиксирует прибыль на пути вверх, но окончательная прибыль от такой торговли, хотя и положительная, будет маленькой.
А что, если цена акции продолжает падать?
На продолжающем падать рынке мы будем постоянно рехеджировать, покупая акции и таким образом сокращая короткую позицию на всем пути вниз. Если акция падает до очень низкого ценового уровня (в данном случае до $70), дельта будет равна нулю, и у нас в этой точке все короткие акции окажутся выкупленными. В данном случае окончательный портфель будет состоять из обесцененного опциона и вообще не иметь в своем составе акций. При очень низких ценах у опциона уже не будет изгиба, из-за чего возможности получения прибыли исчезнут. Продолжение процесса рехеджирования, конечно, зафиксирует прибыль на пути вниз, но, как и при продолжительно растущем рынке, окончательная прибыль торговли, хотя и положительная, будет маленькой.
Какое ценовое движение акции самое лучшее?
Из вышесказанного следует, что тип поведения акции, продуцирующий самую большую прибыль, — это постоянно колеблющиеся цены. Хотя торговля будет давать положительные результаты как при продолжительно растущем, так и при продолжительно падающем рынках, гораздо больше прибыли можно заработать при больших и размашистых колебательных движениях.
Где же ловушка?
Читатель, возможно, уже догадался, что здесь что-то не так. Должна быть какая-то загвоздка в стратегии длинной торговли волатильностью. Не может быть, чтобы в итоге всегда получалась прибыль. В примерах с движением акции от точки "В" к "Z", снова к "В", к "Y' и так далее, мы сделали предположение, которое было удобным для объяснения идеи такой торговли. Предположение состояло в том что, пока цена акции двигалась туда и обратно, время стояло на месте (time stood still). Мы предположили, что опцион не старел. Мы предположили, что профиль опционной цены оставался всегда фиксированной величиной. Каждый раз при прохождении цены акции через интересующую нас точку мы предполагали, что цена опциона всегда одна и та же. Конечно же, такого в обычной жизни не бывает.
Пока цена акции движется от "В" к "Z", потом к "В", далее к "Y' и так 500 раз в день, мы не можем сказать, что профиль опционной цены остается неизменным. В действительности требуется время, чтобы дойти от одной цены до другой. В этом процессе, при прочих равных условиях, опцион всегда теряет свою временную стоимость. Это и есть та самая ловушка. Каждый проходящий день приводит к тому, что профиль цены самого опциона распадается, отходя немного в сторону, двигаясь к изломанной кривой цены, которая прогнозируется к наступлению срока истечения. Нам действительно следует вернуться к вышеупомянутым примерам и установить надлежащую цену опциона, существующую при каждом моменте рехеджирования. Временной распад сократит прибыль от торговли, а в некоторых случаях приведет к чистому убытку. Стратегия действенна, но при должных обстоятельствах. Некая хитрость может определить правильные обстоятельства. Мы вернемся к этому вопросу позже.
4.3 Влияние временного распада - тэта
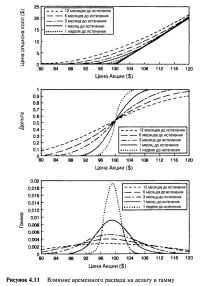
Потеря опционом стоимости с течением времени настолько важна для участников рынка, что ей было отведено специальное название — Тэта (theta). По истечении времени мы говорим, что опцион переживает временной распад, или тэта-распад. Тэта, как и дельта, является еще одним способом измерения чувствительности. Дельта измеряет чувствительность опциона по отношению к цене базовой акции, а тэта измеряет чувствительность по отношению ко времени. Рассматриваемый одногодичный опцион колл с течением времени становится девятимесячным опционом, а затем шестимесячным опционом и так далее. Рисунок 4.4 показывает, как стоимость опциона меняется по отношению к цене акции в разное время до наступления срока. Отдельное множество точек для дальнейшего исследования представлено в Таблице 4.3.
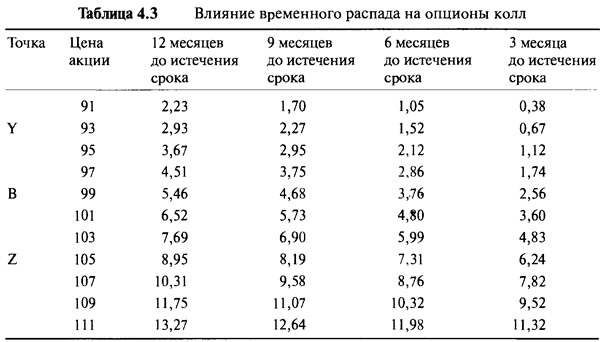
Заметьте, что кривые опционных цен изогнуты и эти кривые постепенно ослабевают, двигаясь по направлению к моменту срока истечения. Рассматривая различные фиксированные цены акции, можно увидеть, какие опционы переживают наиболее сильный временной распад. Расстояние между кривыми представляет собой величину временного распада при каждой цене акции. Кривые находятся дальше всего друг от друга возле цены исполнения и более тесно сгруппированы в отдаленных от нее местах. Понятно, что опционы около денег переживают наибольший временной распад. Чем дальше от цены исполнения, тем меньше влияние временного распада. Опционы глубоко без денег или опционы глубоко в деньгах фактически не имеют вообще никакого временного распада. Это наблюдение, возможно, заставит кого-то подумать о том, что торговец длинной волатильностью должен использовать только те опционы, которые переживают слабый или не имеют вообще никакого временного распада. Однако не все так просто. Сами по себе опционы, не имеющие временного распада, имеют очень небольшой ценовой изгиб. А для волатильной торговли нам нужен именно ценовой изгиб. Опционы с наибольшим ценовым изгибом переживают наибольший временной распад. Опять-таки мы вернемся к этой теме позже.
Временной распад может и зачастую действительно вредит длинной торговле волатильностью. Когда мы прибегаем к такой торговле, то надеемся на возникновение ценовых движений. Любой день, когда цена базового инструмента стоит на месте, является днем потери временной стоимости. Если рынок, в который вы вовлечены, полностью застаивается, тогда убытки растут из-за временной коррозии. Торговцы длинной волатильностью в таких ситуациях говорят, что они "обескровлены до смерти" через тэту. Полезно будет узнать, какая степень волатильности ценового движения необходима, чтобы покрыть стоимость временного распада. Существует несколько способов выяснить это, и для того, чтобы показать только два из них, мы снова вернемся к первоначальной ситуации, которую разбирали выше. Вначале портфель содержит одногодичный опцион колл, оцененный в $5,46, и короткую позицию из 50 акций по $99. Мы в точке "В".
Движение в одном направлении
Рассмотрим движение цены от "В" к "Z", которое обеспечило изменение в $6. Если движение идет без замедления, мы знаем, что получим прибыль. Но что, если движение займет две недели или два месяца? В качестве такого примера на Рисунке 4.5 и в Таблице 4.3 представлена ситуация, в которой движение занимает три месяца. Мы видим, что при цене акции в $105 опцион, у которого осталось только девять месяцев жизни до истечения срока, будет оценен в $8,19 (не $8,95). Кривая опционной стоимости настолько сильно соскользнула вниз, что прибыли стало явно недостаточно для того, чтобы покрыть убытки по акции. Прямая линия цены акции теперь над стоимостью опциона, и это означает окончательный убыток. Стоимость нового опционного контракта на 100х(8,95-8,19)=$76 ниже стоимости контракта, использованного в простом описании торговли без учета временной стоимости. Так что же произошло такого, что прибыль в $49 обернулась прибылью в $49-$76= -$27, то есть убытком? Каково должно быть движение в одном направлении, чтобы мы смогли получить прибыль? Из Рисунка 4.5, становится понятно, что если цена продвинулась до $106 за три месяца, торговая позиция достигнет уровня безубыточности. Если цена продвинется выше, тогда в результате получится прибыль. Можно следовать той же логике и в отношении движения вниз. Вычерчивая кривые стоимостей опциона в различных периодах времени, можно понять, как должен будет двигаться базовый инструмент, чтобы в результате возникла прибыль.
Ценовые колебания
Другой пример может дать представление о том, сколько необходимо ценовых колебаний (с рехеджированием), чтобы покрыть будущий временной распад. Обратимся к Таблице 3.4 снова. Предположим, цена основного инструмента двигается первоначально сложным образом: от "В" к "Z", снова к "В", к "Y1 и так далее. Выше мы посчитали, что каждый путь от "В" до "Z" и опять к "В" приносит прибыль в $96. Если этот путь занял три месяца, то мы увидим, что опцион в точке "В" будет оцениваться в $4,68, упав в стоимости на $5,46-$4,68=$0,78, или $78 за один контракт. Волатильность и рехеджирование помогли получить $96, но временная стоимость составляет $78, поэтому чистая прибыль будет $96-$78=$18. Можно пользоваться этим примером при различных сценариях, чтобы получить представление о типе ценовых колебаний, необходимых для достижения прибыли.
Частота рехеджирований
В рассматриваемом примере мы рехеджируем всякий раз, когда цена акции изменяется на $6. Что если, начиная с точки "В", цена акции никогда уже не окажется в точках "Z" или "Y", или просто не достигнет точки рехеджирования? Нет рехеджирования, значит нет и прибыли от рехеджирования, и поскольку в любом случае существует процесс временного распада опциона, мы фактически останемся в убытке. С другой стороны, рассмотрим ситуацию, когда цена акции колеблется через точку "В" каждый раз намного сильнее. Скажем, цена акции продолжает нормально двигаться, проходя "Z" и "Y", прежде чем вернуться к точке "В". В таком случае нам, очевидно, следует задержать рехеджирование до той поры, пока цена акции не достигнет максимума и минимума каждого колебания. Таким образом, каждое рехеджирование будет приводить к большей прибыли. Проблема состоит в том, что мы не знаем, насколько далеко продвинется цена акции. Если бы мы знали, то не утомляли бы себя предположениями.
Проблема сводится к одному заключению. Более частое рехеджирование фиксирует прибыль благодаря небольшим колебаниям цены, но его недостаток в том, что оно может упустить действительно большую прибыль при больших ценовых колебаниях. Менее частое рехеджирование расширяет границы для большой прибыли, но в то же самое время означает, что будет упущена небольшая прибыль, связанная с маленькими колебаниями цены.
Есть два момента, которые нужно учитывать, — это стоимости рехеджирований и вероятные последствия временного распада. В действительности вряд ли кто-то будет связываться с портфелем, состоящим только из одного опциона. Более реальной будет ситуация, если скажем, портфель состоит из длинной позиции на 100 опционов и короткой позиции на 5.000 акций. Работая с большим портфелем, рехеджирования можно добиться, подгоняя объем опционных контрактов или акций, а издержки, такие как бид-аск спрэд, взносы и комиссионные, будут диктовать, в какую сторону нужно осуществлять подгонку. Выбор стратегии рехеджирования связан с компромиссом. Если стоимости сделок высокие (в случае с опционами на акции), то необходимо будет ждать значительного движения цены акции, чтобы оправдать расходы по сделке. Если стоимости сделок низкие (как в опционах на фьючерсы), тогда рехеджирование может быть достаточно частым.
4.4 Альтернативный взгляд на справедливую стоимость опциона
В третьей главе мы говорили о справедливой стоимости опциона и объясняли ее с точки зрения его среднего значения на длительном временном промежутке. Была проведена аналогия с игрой в кости, чтобы объяснить понятие возможной стоимости, или ожидаемой стоимости.
Для того чтобы посчитать справедливую стоимость, необходимо иметь представление о вероятностных значениях цены акции при наступлении срока истечения опциона. Тогда при наступлении срока очень легко обнаружить справедливую стоимость опциона: если это опцион в деньгах, то его стоимость будет равна внутренней стоимости, а если это опцион без денег, то он ничего не будет стоить. Принимая во внимания все результаты, полученные при данном распределении цен акции, нетрудно было угадать ожидаемую стоимость. Мы определили эту ожидаемую стоимость как стоимость, равную такой цене, которую необходимо заплатить за опцион, если в долгосрочном промежутке времени мы хотим достичь уровня безубыточности. Понятие долгосрочный промежуток времени можно объяснить на двух примерах.
- 1. В первом примере опционный игрок постоянно покупает опционы по справедливой цене и ждет истечения их срока. Иногда по истечении срока опцион чего-то стоит, а иногда ничего не стоит. Если игрок постоянно платит справедливую стоимость, его "заработки" только покроют его ставки — он останется безубыточным.
- 2. В другом примере опционному игроку предлагают большое количество различных опционов, имеющих в будущем одну и ту же дату истечения срока. Если игрок купит все опционы сразу и заплатит за каждый из них правильную справедливую стоимость, тогда доход при наступлении срока сравняется со всеми его затратами, и он останется безубыточным.
В обоих случаях при толковании справедливой стоимости опциона мы предполагаем, что игрок покупает опцион и держит его до наступления срока. Между датой покупки и датой истечения срока игрок просто наблюдает, как стоимость его позиции меняется каждый день, но ничего не предпринимает. В такой интерпретации справедливой стоимости опциона участник играет пассивную роль. Ему либо повезет, если цена акции значительно поднимется, либо он проиграет свою ставку.
Длинная волатильная стратегия теперь позволяет нам рассмотреть другое понятие справедливой стоимости опциона. Представим, что игрок составил дельта-нейтральный портфель, указанный выше, и ждет какого-нибудь эффекта от волатильности. Предположим, что расходы по сделке очень небольшие или равны нулю. При отсутствии затрат игрок длинной волатильностью может позволить себе рехеджироваться так часто, как ему этого захочется. Скажем, он решил, что будет рехеджировать каждый раз при изменении цены основного инструмента на небольшое значение, например, на 10 центов. Выиграет он или проиграет?
Ответ зависит от первоначальной цены и последующей волатильности. Если стартовая цена низкая, а фактическая волатильность высокая, игрок выиграет. Если цена высокая, а фактическая волатильность низкая, то игрок проиграет. Если он многократно исполняет сделку, то за длительный промежуток времени в среднем возникает рехеджированный доход. Если доход в длительном промежутке времени в точности совпадает с оплаченной ценой, тогда можно сказать, что цена опциона действительно была справедливой с точки зрения волатильности. Отсюда мы имеем еще одну возможность понять, дорогой это опцион или нет.
Какую правильную справедливую стоимость надо использовать? Есть два подхода к оценке справедливой стоимости. Первый — пассивный: покупка и удержание опциона до наступления срока истечения. Второй -активный, включающий в себя продолжительное динамичное рехеджирование. Примечательно, что оба подхода дают один и тот же ответ. Есть только одна справедливая стоимость, но два разных толкования, и причина этого не так сложна, как кажется на первый взгляд. Ключ к пониманию того, почему два разных подхода дают одну и ту же справедливую стоимость, лежит в более подробном рассмотрении распределения цены основного инструмента. Во второй и третьей главах мы использовали разные модели поведения цены акции для объяснения различных понятий.
Во второй главе мы говорили об измерении волатильности. Чтобы понять, как измеряется волатильность, мы изучали развитие цены определенной акции изо дня в день. Было показано, что волатильность может рассматриваться как функция следования ежедневным ценовым изменениям. Нас не интересовало, куда в конце концов, двигалась цена акции -нам было интересно, как она двигалась. При измерении волатильности нас интересовала только величина положительных и отрицательных ценовых изменений.
В третьей главе мы говорили также и о справедливой стоимости опциона колл, показав должный изгиб линии цены. Для этого мы обратились к другому аспекту распределения цены, лежащей в основе опциона акции. Справедливая стоимость была показана как простое вероятностное среднее значение цены опциона в один день — день истечения срока. Цена опциона при истечении срока является прямой функцией цены акции в день истечения срока, поэтому нам нужна была информация только о распределении цены акции в этот день. Этот подход полностью игнорирует путь, по которому двигается цена до наступления срока, — он использует только окончательную цену в день истечения срока.
В этом и состоит разница между двумя подходами. Статическая модель справедливой стоимости использует информацию о распределении цены акции в один день в будущем, тогда как справедливая стоимость длинной волатильности вычисляется на основе информации о ежедневных колебаниях цены, полностью игнорируя будущую цену при наступлении срока. Оба подхода дадут одну и ту же справедливую стоимость, если предположить одинаковое распределение цены, лежащей в основе акции. Если мы предположим, что релевантное распределение является логнормальным и что использованное измерение дисперсии равно ожидаемой волатильности, тогда оба метода, обеспечивающие оценку справедливой стоимости, дадут одинаковые результаты. Если показатель волатильности будет высоким (низким), тогда обе справедливые стоимости будут высокими (низкими). Волатильность ежедневных ценовых изменений прямо воздействует на распределение цен при наступлении срока. Если волатильность высокая, то распределение цен акции в день истечения срока будет очень рассредоточенным. Если волатильность высокая, тогда намного больше вероятность того, что заканчивающий жизнь опцион находится глубоко в деньгах, а потому стоит дорого. Поэтому опцион на высоковолатильную акцию должен иметь более высокую справедливую стоимость даже тогда, когда рассматривается статичная стратегия покупки и удержания.
Есть еще одна, заключительная деталь, объясняющая разницу между двумя подходами к определению справедливой стоимости. Скажем, мы точно знаем, что рассматриваемая акция будет демонстрировать волатильность 15% в обозримом будущем. Рассмотрим поведение двух участников рынка, покупающих одногодичный опцион колл и платящих правильную справедливую стоимость, рассчитанную с помощью модели Блэка-Шоулза при значении волатильности в 15%. Первый игрок следует стратегии покупки и удержания, а второй — дельта-нейтральной длинной стратегии на волатильность. Скажем, цена акции в самом начале равна $99, а цена исполнения — $100. Рассматриваемый опцион — тот, который мы изучали на протяжении этой главы, поэтому его цену мы уже знаем. Она составляет $5,46 или $546 за контракт. Оба игрока должны за длительный период времени оказаться безубыточными. Предположим, что цена акции к моменту истечения срока составляет $90. Первый игрок целиком потеряет всю свою ставку в $546, но игрок волатильностью возместит свои затраты в $546 за счет всей рехеджированной прибыли. Первый участник рынка потеряет 100% своей инвестиции, а второй достигнет уровня безубыточности. И оба заплатили правильную справедливую стоимость. Как такое может быть? Представим, что обоим была дана вторая попытка при тех же самых инвестиционных стратегиях. Но на этот раз цена акции должна закончить свой путь, скажем на $114 и при этом опцион финиширует при стоимости в $14 или $1.400 за контракт. Первый игрок закончит с $1.400, в то время как второй закончит с $546. При второй попытке стратегия покупки и удержания принесет 1.400-546=$854, а волатильная стратегия приведет к уровню безубыточности. В этом фактически вся разница между двумя подходами к определению справедливой стоимости. В первом подходе безубыточность рассматривается с точки зрения среднего значения за длительный период времени, а во втором безубыточность присутствует всякий раз.
4.5 Волатильность и вега
Модель Блэка-Шоулза является сложным уравнением, требующим ввода определенной информации. Эта информация обычно используется в качестве параметров и для опционов на те акции, по которым дивиденды не оплачиваются. Они таковы: (1) цена акции, (2) цена исполнения, (3) время до истечения срока, (4) процентная ставка (если это имеет значение в текущих обстоятельствах) и (5) волатильность цены акции. Как и во всех математических моделях, результирующие величины действительны только при условии, если введенная информация была правильной. Ошибка или неточность в исходной информации обязательно отразится на результате. Первые три переменные полностью и объективно оцениваемы, а четвертая, хотя и нефиксированная, как правило, довольно стабильна на протяжении всей жизни опциона. Волатильность не столь очевидна, и здесь необходимо прибегнуть к использованию исторической оценки или субъективного заключения. Если применяемое значение волатильности слишком высокое (низкое), тогда модель даст завышенную (заниженную) справедливую стоимость. Таблица 4.4 и Рисунок 4.6 показывают результаты использования различных данных по волатильности применительно к рассматриваемому одногодичному опциону колл.
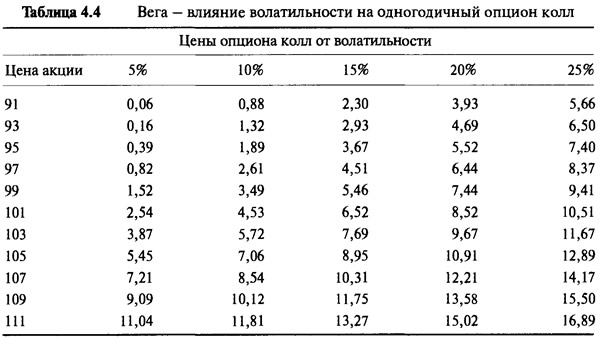
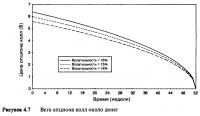
Чувствительность цен опциона к изменению волатильности сходна с чувствительностью ко времени. Опционы около денег наиболее чувствительны, а опционы глубоко без денег и глубоко в деньгах менее чувствительны. Цифры показывают важность получения правильных данных о волатильности. Стандартная длинная торговля волатильностью объяснялась на примере использования установленной волатильности в 15%. Вначале при цене акции в $99 опцион был оценен в $5,46. Если сразу же после начала торговли рынок оценил бы все одногодичные опционы исходя из того, что будущая волатильность составит только 10%, то мы могли увидеть, что цена опциона незамедлительно упала бы до $3,49, что на практике автоматически ведет к убыткам безо всяких на то особых причин. Чувствительность цен опциона к изменению волатильности настолько важна для участников рынка, что для нее было найдено специальное определение. Скорость изменения цены опциона относительно волатильности называется Вегой (vega). Обычно вега определяется как изменение цены опциона, вызванное изменением волатильности на 1%. При акции на $99 рассматриваемый опцион имеет вегу в $0,40, при $120 вега составляет $0,20, а при $80 вега составила бы $0,13. Вега опциона изменяется не только вместе с ценой базовой акции, но и вместе со временем, оставшимся до истечения срока. При прочих равных условиях опционы с меньшим временем до истечения срока менее чувствительны к волатильности — эти опционы имеют более низкую вегу. Лучше всего это можно доказать, изучив изменение цены опциона во времени при фиксированной цене акции, но при различной волатильности. Рисунок 4.7 показывает ситуацию с опционами около денег. На графике видно, что вега опциона равна расстоянию между кривой 15% и кривой 14% либо кривой 16%. Заметьте, что по мере истечения срока кривые сходятся. По мере того, как время движется, опционы становятся все менее чувствительными к изменениям волатильности или изменчивости оценки волатильности. Точная оценка волатильности крайне важна для опционов с очень большим временем до истечения срока и фактически не имеет значения для опционов с маленьким временем до истечения срока.
4.6 Подразумеваемая волатильность
Теперь должно стать очевидным, что значение волатильности является ключевым моментом для игрока длинной волатильностью. Если полагать, что в будущем волатильность составит 15%, тогда при цене акции в $99 безубыточная цена опциона равна $5,46. Для того чтобы получить прибыль, фактически необходимо входить при более низких ценах или надеяться, что будущая волатильность будет выше 15%. На языке рынка мы говорим, что цена $5,46 подразумевает будущую 15-процентную волатильность или что 15% есть подразумеваемая волатильность (implied volatility) опциона. Покупка опциона по $5,46, по сути, является выплатой вперед за всю будущую рехеджированную прибыль, связанную с 15-процентной волатильностью цены акции. И тогда мы говорим, что покупаем волатильность по 15% (buying volatility).
Теперь рассмотрим иную ситуацию. Другая акция по цене $109 тоже имеет одногодичный опцион колл с ценой исполнения $100. Опцион предлагается по цене $10,12. Изучение Таблицы 4.4 показывает, что эта цена подразумевает только 10-процентную волатильность. Этот опцион требует только 10-процентную будущую волатильность цены акции для достижения уровня безубыточности. Если две рассматриваемых акции при их сравнении продемонстрируют сходную волатильность, то мы можем сказать, что опцион по $10,12 дешевле опциона по $5,46. Новый опцион, хотя и намного дороже в долларовом выражении, с точки зрения волатильности дешевле первого опциона. Итак, подразумеваемая волатильность может быть использована в качестве измерителя относительной стоимости. Опционы с различным временем до истечения срока, различными ценами акций и различными ценами исполнения можно сравнивать, используя подразумеваемую волатильность.
Как вычислять подразумеваемую волатильность? В действительности совсем не обязательно утруждать себя вычислением подразумеваемой волатильности, так как можно воспользоваться "он-лайн" услугами большинства информационных служб, которые производят расчеты, связанные с опционами. Хотя следует обратить внимание на то, что процесс вычисления относительно прост. Как ранее говорилось, первые четыре параметра известны. Единственное, что неизвестно, так это — волатильность. Несомненно, известна и рыночная цена опциона. Для того чтобы выяснить подразумеваемую волатильность, надо сделать следующее. Подставьте известные четыре значения в модель. Попробуйте подставить любое значение волатильности, скажем 25%, и посчитайте цену, согласно модели. Потом задайте себе вопрос: стоимость модели та же самая, что и рыночная стоимость? Если ответ "да", тогда подразумеваемая волатильность опциона равна 25%. Если ответ "нет", тогда попытайтесь подставить другое значение, скажем 24% или 26%, и повторите процедуру заново. В конце концов, вы получите волатильность, которая даст цену модели, в точности совпадающую с рыночной ценой. В качестве примера пусть это будет 12%. И эта величина как раз и является подразумеваемой волатильностью опциона. Мы говорим, что рыночная цена опциона подразумевает (если модель действенна), что будущая волатильность будет 12%. Процедура подбора различных значений может показаться обременительной и непродуманной, но на самом деле это не так. Существуют хорошо известные математические методы, которые дают быстрые и точные результаты.
4.7 Значение изгиба и гамма
В ситуации, которую мы рассматривали в разделе 4.2, когда цена акции подходящим образом колебалась туда и обратно, мы намеренно выбрали центром колебаний точку "В". Прибыль от волатильной торговли — и на самом деле только от нее — получается благодаря изгибу опционной цены. А линия цены изогнута только благодаря загибу, возникающему при истечении срока обращения опциона. Должно быть очевидно, что при данном движении цены акции, скажем на х %, чем изогнутей линия, тем значительней рехеджированная прибыль. Другими словами, можно добиться той же самой рехеджированной прибыли при меньшем движении цены акции, но с опционом, который обладает более значительной степенью изгиба. Игрок длинной волатильностью всегда надеется на изгиб при низких ценах опциона. Изгиб настолько важен для опционного рынка, что ему тоже было дано специальное название, только уже от другой греческой буквы — гамма (gamma). Это понятие наилучшим образом раскрывается при изучении двух воображаемых кривых опциона, которые представлены на Рисунке 4.8.
Две кривые на Рисунке 4.8 специально выбраны таким образом, чтобы их наклоны в точке "В" были одинаковы. Кривая (2) отклоняется от касательной прямой линии быстрее, чем кривая (1), и очевидно, приведет к большей рехеджированной прибыли. Также мы можем использовать Рисунок 4.8 для неточного определения изгиба с точки зрения наклонов. Понятно, что в точке "В" наклоны обеих кривых одинаковы, а при более низких ценах акции у кривой (2) наклон меньше, чем у кривой (1), но при высоких ценах акции у кривой (2) наклон больше, чем у кривой (1). По мере того, как цена базовой акции увеличивается, обе кривые увеличивают наклоны, но наклон кривой (2) возрастает с большей скоростью. Таким образом, мы получаем определение изгиба — это скорость изменения наклона. Так как наклоном кривой является дельта, то мы говорим, что изгиб — это скорость изменения дельты. Гкмма опциона является скоростью изменения дельты. Вначале это может показаться довольно сложным, так как дельта сама является скоростью изменения. Дельта — скорость изменения цены опциона относительно цены базовой акции. Поэтому гамма — это скорость изменения скорости изменения цены опциона относительно цены акции. Чем пытаться объяснить это с точки зрения различных уровней скоростей изменения, легче рассматривать гамму с точки зрения кривых и помнить, что опционы с более высокой гаммой обеспечивают большую рехеджированную прибыль.
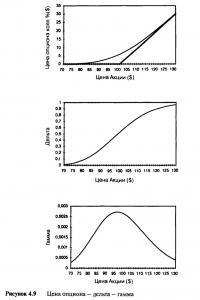
Графическое представление гаммы одногодичного опциона колл дано на Рисунке 4.9. Первый рисунок показывает цену опциона. Второй показывает дельту, или наклон первой кривой. Третий рисунок показывает гамму, или наклон второй кривой. Можно рассматривать гамму на основе поведения ценовой кривой или кривой дельты. В привязке к ценовой кривой мы можем видеть, что глубоко в деньгах и глубоко без денег профиль цены почти прямой или изогнут совсем немного. Максимальный изгиб можно наблюдать при ситуации около денег. С точки зрения линии дельты мы можем видеть, что максимальный наклон бывает в состоянии около денег, а при очень высоких и низких ценах наклон кривой дельты небольшой. Заметьте также, что гамма длинного опциона колл является положительным числом, и это потому, что по мере увеличения цены базовой акции то же самое делает и наклон кривой линии цены. Кривые цен с наклоном вверх всегда имеют положительные гаммы.
Точным математическим определением гаммы является мгновенная скорость изменения дельты. На практике легче всего рассматривать изменения дельты, вызванные небольшими изменениями цены акции. Реальная польза гаммы для опционного трейдера и игрока волатильностью — в оценке будущих результатов рехеджирования. Гамма является изменением дельты, связанной с изменением цены базового инструмента, поэтому гамма также является способом измерения скорости, с которой мы рехеджируем дельта-нейтральную позицию. Таблица 4.5 демонстрирует ситуацию с портфелем, содержащим 100 опционов. Каждый опцион может быть исполнен на 100 акций, поэтому для этого портфеля все дельты и гаммы помножены на 100x100=10.000. Мы произвольно определяем здесь гамму, основываясь на изменении в дельте, которое происходит при движении в $0,10 в базовом инструменте.
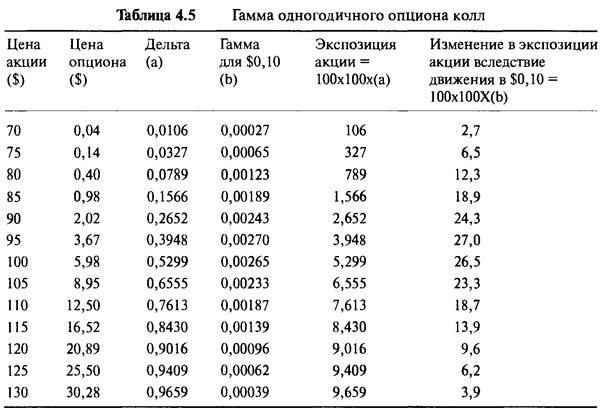
Посмотрим на строку $80, описывающую вывод значения гаммы. При этой цене 100 опционов требуют коротких позиций на 789 акций, чтобы полностью достичь дельта-нейтрального положения. При этой цене гамма равна 12,3 единицам, и маленькие ценовые изменения в $0,10 потребуют рехеджирования путем вычитания или прибавления 12 акций. При цене $95 гамма составляет 27 единиц, и подобные маленькие ценовые изменения в $0,10 потребуют рехеджирования путем вычитания или прибавления 27 акций. Длинная торговля волатильностью создает прибыль благодаря изгибу, и эта прибыль фиксируется с помощью процесса рехеджирования. Поэтому гамма позиции является непосредственным измерением потенциальной прибыли вследствие волатильности, и зачастую термин "длинная гамма" (long gamma) используется вместо термина "длинная волатильность". Термин длинная гамма подразумевает, что гамма позиции положительна. Мы можем увидеть из Рисунка 4.9 и Таблицы 4.5, что самая потенциально интересная, как самая высокая, гамма возникает у опционов около денег. К сожалению, это именно те опционы, которые переживают наибольший распад теты.
4.8 Временной распад влияет на дельту и гамму
Все опционы до истечения срока имеют кривой профиль цены. В любой момент времени наклон дельта кривой дает возможность оценить эквивалентность акции через экспозицию. В любой момент времени изгиб (гамма) измеряет, насколько быстро меняется экспозиция акции. По мере истечения срока жизни, опционы ослабевают во времени и к истечению своего срока достигают изогнутую линию цены. Полезно будет рассмотреть подробней, как меняются со временем дельта и гамма на различных отрезках кривой. Это можно сделать, не используя традиционный метод сложных вычислений, а просто посмотрев на разрывы трех отрезков кривых опциона, которые видны на Рисунке 4.10, а затем снова рассмотрев портфель из длинной позиции на 100 опционов.
Опционы без денег
Для упрощения предположим, что с течением времени опцион остается в состоянии без денег. Мы видим, что наклон кривой и степень изгиба постепенно приближаются к нулю. Течение времени приводит к уменьшению экспозиции по акции (дельты) и скорости изменения экспозиции по акции (гаммы). Поэтому опцион в состоянии без денег, подходя к своему сроку истечения, приводит к постепенному сокращению степени хеджирования акции. Достигая срока истечения, наклон рехеджирования, или переустанавливающее воздействие дельты будет уменьшаться.
Опционы в деньгах
Течение времени приводит к постепенному увеличению наклона кривой. К моменту истечения срока опциона кривая совпадает с линией паритетности. В пределе дельта достигает 1,0 и опцион становится неотличимым от акции. Изгиб также постепенно уменьшается. Поэтому длинная волатильная позиция, находясь в деньгах и приближаясь к своему сроку истечения, приводит к постепенному увеличению степени хеджа акции до тех пор, пока при наступлении срока длинная и короткая позиции не совпадут друг с другом один к одному. Как и в случае с опционами без денег, при подходе срока истечения гамма уменьшается, поэтому и наклон рехеджирования тоже уменьшается.
Опционы вблизи около денег
Самый интересный аспект опционов около денег при истечении срока заключается в том, что изгиб увеличивается по мере приближения все ближе и ближе к последнему изгибу, в результате чего наклон рехеджирования увеличивается. Таблица 4.6 перечисляет максимальные точки изгиба для различных опционов, представленных на Рисунке 4.10. При сроке в один год до истечения опциона максимальная гамма составляет 27 и соответствует цене $97. Когда остается одна неделя до срока истечения, она увеличивается до 192 и соотносится уже с ценой $99,8. При годовом сроке до истечения ценовое изменение на $0,10 потребует рехеджирования 27 акциями, но при одной неделе до срока истечения то же самое ценовое движение потребует 192 акции. Оканчивающие свой срок жизни опционы в состоянии около денег имеют большие гаммы, и это потому, что дельта может колебаться от 0,0, когда опцион совсем немного без денег, до 1,0, когда опцион немного в деньгах. В качестве экстремального случая рассмотрим опцион, заканчивающийся через минуту. Почти при любой цене, ниже $100, скажем $99,5, опцион должен быть абсолютно нечувствительным к ценовым изменениям акции, его дельта будет 0,0. Почти при любой цене свыше $100, скажем $100,5, опцион должен вести себя точно как акция, и его дельта будет 1,0. Если в ближайшие минуты перед окончанием цикла жизни опциона цена акции движется вверх или вниз относительно цены исполнения, тогда рехеджирование будет огромным. В одну секунду хедж может потребовать ввод позиции на 10.000 акций шорт, а в другую он может оказаться уже нулевым. Каждый раз при небольшом увеличении цены акции надо будет продавать в шорт 10.000 акций и покупать их обратно, как только цена совсем немного упадет. Подобная ситуация — настоящая мечта игрока длинной волатильностью.
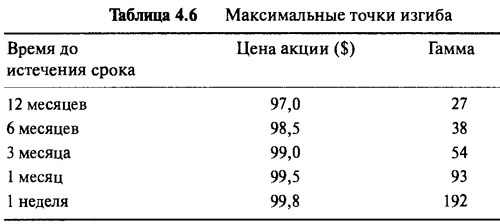
Итак, без использования расчетов, на основании Рисунка 4.10, мы подводим итог относительно трех аспектов чувствительности цены опциона колл:
- 1. Постепенно разрушающийся ценовой уровень показывает различные степени временного распада (тэта).
- 2. То, как увеличивается (уменьшается) наклон кривой опционов без денег (в деньгах), демонстрирует изменение чувствительности цены опциона (дельты) во времени.
- 3. Изгиб (гамма), или изменение в чувствительности максимально около денег и увеличивается с приближением срока истечения.
Эти выводы подкрепляются графиками цен, дельты и гаммы различных опционов в трех "окошках" на Рисунке 4.11.
4.9 Контур дельты
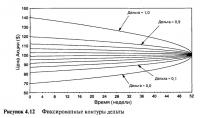
Другим способом показать изменения дельты и гаммы во времени является карта контура дельты. На Рисунке 4.12 отмечены точки, определяющие цены акции в привязке к временной карте, на которой дельты опционов имеют фиксированные значения. Для ясности мы показываем только 11 контуров. Каждый контур включает все точки, которым соответствует определенная величина дельты. 11 контуров описывают дельты, начинающиеся с 0,0 и увеличивающиеся на равное значение, равное 0,1, и так до 1,0. Вдоль самого нижнего контура дельта равна 0,0, а вдоль второго снизу контура дельта составляет 0,1 и — так далее. Самый верхний контур соответствует дельте 1,0.
Существует несколько способов прочтения графика. Рассмотрим прямую горизонтальную линию, проведенную через ценовой уровень $90. Это говорит о том, что цена базовой акции остается постоянно на уровне $90 до срока истечения действия опциона. В самом начале (время = 0) с одним годом в будущем мы видим, что опцион имеет дельту между 0,2 и 0,1. С течением времени, если цена акции остается постоянной, то прямая линия оказывается все ниже и ниже в территории дельты до тех пор, пока приблизительно через 47 недель (5 недель до истечения срока) линия не попадает в 0,0 дельта-зону. С течением времени дельты опционов без денег уменьшаются. Если рассматривать прямую горизонтальную линию, проведенную через ценовой уровень $110, то можно увидеть ситуацию с точностью до наоборот. Линия будет входить все выше и выше в контуры дельты, в итоге войдя в 1,0 дельта-зону. С течением времени дельты опционов в деньгах увеличиваются. В этом мнении нас еще раз укрепляет наблюдение за кривыми линий цен опционов на Рисунке 4.10.
Графики на Рисунке 4.12 также могут продемонстрировать, как изменяется рехеджирование в момент приближения срока истечения. Если мы нанесем обычные ценовые ряды акции на ту же самую контурную карту опциона, то сможем увидеть, что происходит с портфелем длинной волатильности.
По мере движения цены акции во времени контуры дают точное отражение состояния портфеля. Портфель первоначально дельта-нейтральный, и по мере роста или падения цены акции контуры могут отражать степень отсутствия нейтральности. Скажем, первоначальная дельта равна 0,5, а потом цена акции начинает расти. При пересечении контуров дельты все выше и выше портфель становится все больше и больше несбалансированным на длинной стороне. Это и будут точки, в которых должна наступать ребалансировка в зависимости от стратегии рехеджирования. Фактически можно использовать контуры для обозначения срока рехеджирования. Если мы произвольно решим, что можем регулировать рехеджирование акции только тогда, когда дельта изменяется, скажем на 0,10, то в этом случае каждый раз, когда цена акции будет пересекать один из фиксированных контуров, мы будем рехеджировать. Таким образом, возможно отразить на традиционном ценовом графике акции от времени каждую рехеджированную сделку.
При сроке в один год до окончания жизни опциона расстояние между контурами рехеджирования (с точки зрения цены акции) большое, и активность там, возможно, небольшая. С течением времени контуры сходятся в одну точку, и цена акции устанавливается близко к цене исполнения $100, обеспечивая тем самым оживление процесса рехеджирования. При сроке истечения через один год цена акции движется от $97 до $103 и пересекает один контур. Двигаясь тем же самым путем, но при трех месяцах до истечения срока, она пересечет семь контуров. Эти графики также показывают важность расстояния (в долларовом выражении) между ценой акции и ценой исполнения в различное время до истечения срока. При сроке в один год до срока истечения цена акции может быть выше на $40 цены исполнения, а опцион все еще имеет возможность обеспечить полезную рехеджированную прибыль. При трех месяцах до истечения срока полезный диапазон сокращается до $12.
4.10 Три моделирования
Теперь мы можем продемонстрировать некоторые модели длинной торговли волатильностью. Три различных произвольных ценовых ряда были выведены с помощью меняющейся волатильности базового инструмента. Предположим, что рассматриваемый опцион был первоначально оценен, исходя из будущей волатильности 15%. Каждый ряд начинается с цены акции, установившейся на $100, а опцион оценивается в $5,98. Для упрощения мы будем использовать вышеописанное торговое правило и осуществлять корректировку, только когда дельта опциона меняется на 0,10.
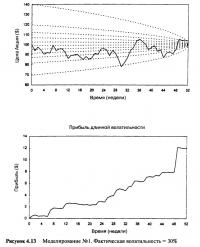
Рисунок 4.13 показывает ситуацию, когда волатильность базового инструмента равна 30%. Цена акции пересекает контурные линии много раз, и каждый раз производится корректирующее хеджирование акции. Каждый раз при хеджировании фиксируется маленькая прибыль. Нижний рисунок показывает постепенное суммирование всей прибыли. Это особое моделирование показывает большую прибыль не только из-за высокой волатильности, но и из-за того, что траектория цены акции оказалась в зоне высокой гаммы как раз перед истечением срока. Последний подъем прибыли за последние пять недель явился следствием движения цены акции через 9 из 11 контуров. За последние пять недель портфель рехеджировался девять раз.
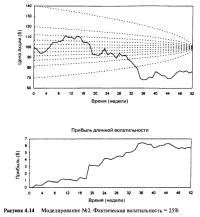
Рисунок 4.14 отражает ситуацию, в которой волатильность базового инструмента составляет 25%. Это выше, чем было заплачено, поэтому все еще наблюдается прибыль. Этот ряд имеет отрицательное перемещение (drift), и после 34 недель цена акции настолько низка, что дельта опциона равна нулю. После точки, фиксирующей 34 недели, траектория акции уже больше не входит в полезную зону, и поэтому больше никакой прибыли не возникает.
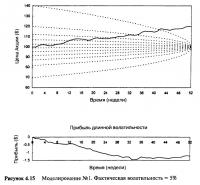
Рисунок 4.15 отражает ситуацию, в которой волатильность основного инструмента равна 5%. Этот ряд имеет положительную тенденцию, поэтому рехеджирование будет идти в одном направлении — посредством продажи акций на пути наверх. Как и на Рисунке 4.14, траектория акции блуждает в бесполезной зоне и больше не возвращается. Это как раз та ситуация, в которой наблюдается волатильность меньше той, за которую было заплачено. Окончательный убыток в третьем моделировании составил $1,45 или $145 за контракт.
4.11 Влияние веги на дельту и гамму
Во всех вышеперечисленных ситуациях мы предполагали, что параметр волатильности, используемый профессионалами рынка, оставался фиксированным на протяжении всей жизни опциона. Но чаще всего так не бывает. В середине жизни опциона участники рынка могут вдруг осознать, что будущая волатильность собирается падать. В такой ситуации, при прочих равных условиях цена опциона будет придерживаться нижней кривой. Это показано на Рисунке 4.6, и на основании тщательного исследования кривых можно сделать вывод, что изменения в дельте и гамме вследствие движений волатильности почти сходны с изменениями, происходящими под влиянием времени.
Падающая волатильность (falling volatility) даст результат, сходный с воздействием времени, а именно:
- 1. Постепенно снижающийся ценовой уровень опциона с наиболее ярко выраженным падением в состоянии близко около денег.
- 2. Опционы далеко без денег будут иметь уменьшающиеся дельты и уменьшающиеся гаммы.
- 3. Опционы глубоко в деньгах будут иметь увеличивающиеся дельты и уменьшающиеся гаммы.
- 4. Опционы около денег будут иметь увеличивающиеся гаммы.
Для игрока длинной волатильностью это может быть или хорошей, или плохой новостью. Какова бы ни была ситуация, портфель будет переживать немедленную переоценку потерь вследствие падения цены опциона. Однако если цена акции близка к цене исполнения, тогда увеличение гаммы фактически может означать больший простор для рехеджирования, чем раньше. Несмотря на то, что могут возникнуть и первоначальные убытки, они способны быть больше, нежели компенсация от возросшей вероятности будущего рехеджирования. Мы говорили о спаде в волатильности. А что произойдет, если будет наблюдаться неожиданный подъем волатильности?
При поднимающейся волатильности (increasing volatility) эффект будет обратным, а именно:
- 1. Постепенно поднимающийся ценовой уровень опциона с наиболее выраженным ростом в состоянии около денег.
- 2. Опционы далеко без денег будут иметь увеличивающиеся дельты и увеличивающиеся гаммы.
- 3. Опционы глубоко в деньгах будут иметь уменьшающиеся дельты и увеличивающиеся гаммы.
- 4. Опционы около денег будут иметь уменьшающиеся гаммы.
Понимание всех сложностей влияния цены акции, времени до истечения срока действия опциона и волатильности на цену опциона, дельту и гамму является существенным моментом в управлении волатильной стратегией. Простая длинная стратегия волатильности может принести прибыль при хороших обстоятельствах, равно как и убыток при плохих обстоятельствах. Хорошие обстоятельства - это покупка опционов с относительно низкой подразумеваемой волатильностью, а в последующем - развитие ситуации с высокой волатильностью. Это может означать покупку 25% волатильности и получение в дальнейшем 35% волатильности или покупку 5% волатильности и получение в дальнейшем 15% волатильности. Плохие обстоятельства заключаются в покупке игроком, как он полагает, относительно низкой волатильности и получение в дальнейшем еще более низкой волатильности. При любой торговой стратегии важно обдумывать, какие могут быть самые большие победы и какие самые серьезные поражения. Мы должны изучить как лучший, так и худший сценарии.
4.12 В самом худшем случае
Для получения прибыли стратегия нуждается в волатильности, и худший случай — это когда вообще нет никакой волатильности. Существует несколько сценариев, когда ценовой ряд может иметь нулевую волатильность.
Простейший случай — когда цена акции остается совершенно неизменной до истечения срока. С приближением срока истечения условия хеджирования будут изменяться, но все сделки будут происходить при неизменной цене акции, а при истечении срока хеджирование акции будет полностью раскручиваться при одной и той же цене акции. В этой ситуации убыток стратегии становится равным временной стоимости самого опциона. Рисунок 4.16 показывает убытки (тип 1), наблюдаемые при таком типе нулевой волатильности.
При втором типе нулевой волатильности (тип 2), который в действительности может привести к еще большим убыткам, цена акции движется постепенно и методично по направлению к цене исполнения, в точности сливаясь с ней при наступлении срока истечения. Таким образом, опцион обесценится, приведя к общей сумме убытков, равной первоначальной стоимости опциона. Если опцион первоначально был в деньгах, то убытки будут немного возмещены прибылью, полученной от короткой позиции по акции. Если опцион первоначально был без денег, то убытки будут добавлены к короткой позиции по акции. На Рисунке 4.16 графически изображены варианты различных ситуаций.
Для пояснения, мы поработаем с расчетами цены акции, начиная с $120, и цены опциона $20,89. На этих уровнях дельта равна 0,9, поэтому нейтральный портфель будет содержать один опцион и короткую позицию на 90 акций. Мы предположим, что цена акции постепенно падает до $100 ко дню истечения срока. При прочих равных условиях падение цены акций приводит к сокращению величины дельты. Однако из раздела 4.8 мы знаем, что при прочих равных условиях дельта опционов в деньгах увеличивается по мере приближения срока истечения. Ради упрощения расчетов давайте предположим, что влияние падающей цены акции с течением времени сводится на нет и что дельта остается постоянно равной 0,9. Это означает, что дополнительной рехеджированной прибыли не будет и при наступлении срока истечения мы покупаем обратно 90 акций по $100. Хеджирование акции принесло доход 90х(120-100)=$1.800, который возместил убыток опциона в 20,89х100=$2.089. Общая сумма убытка составила $289, что на $200 больше временной стоимости первоначального опциона. Следует заметить, эти еитуации крайне запутаны, и можно выдумать ситуации, при которых убытки будут несколько большими. Важно отметить, что можно посчитать заранее, какие максимальные убытки вероятней всего возникнут. Длинная волатильная стратегия имеет ограниченные убытки (limited loss) и, в худшем случае, можно будет потерять первоначальную стоимость опциона плюс некоторые ограниченные суммы при шорт хедже.
Прежде, чем мы закончим обсуждение самого худшего варианта, интересно будет еще раз задуматься над тем, почему второй из двух вышеописанных сценариев еще хуже первого. Это происходит потому, что во-первых, потеряна полностью вся стоимость опциона, и во-вторых, нет рехеджированной прибыли. Для того, чтобы на момент истечения не было бы абсолютно никакого рехеджирования, дельта опциона должна оставаться постоянной во времени. Мы рассмотрели очень сложную ситуацию, в которой течение времени и движение цены акции имели противоположные влияния на дельту, в результате чего дельта оставалась неизменной. Фактически, эта ситуация такая же, как и на Рисунке 4.12, где представлена диаграмма контура дельты. Теперь мы видим, что можно рассматривать диаграмму контура фиксированной дельты по-разному. Если на протяжении жизни опциона цена акции описывает один из контуров фиксированной дельты, тогда для рехеджирования не будет возможности, в результате чего потери будут соответствовать убытку, обозначенному в одном из худших вариантов на Рисунке 4.16. Понятно, что цена акции должна двигаться по совершенно определенному пути, чтобы в результате получился самый худший вариант.
4.13 В самом лучшем случае
Существует много хороших сценариев, и самый лучший тот, в котором сразу же после начала торга цена акции начинает сильно колебаться вверх и вниз вокруг точки с максимальной гаммой (около денег). Однако есть еще два варианта развития событий, при которых достигается очень большая прибыль. Чтобы понять, в каких ситуациях это происходит, рассмотрим еще раз первоначальный дельта-нейтральный портфель, приведенный в Таблице 4.2. Цена акции равна $99, цена опциона $5,46, а коэффициент хеджа (дельта) равен 0,5. Портфель состоит из длинной позиции на один опцион колл и короткой позиции на 50 акций. Мы знаем, что, если цена акции будет двигаться в ту или в другую сторону от $99, возникнет прибыль.
A. Крах рынка
Предположим, что сразу же после начала торга цена акции внезапно падает на $60 — до $39. На уровне $39 опцион будет настолько далеко без денег, что будет обесценен, поэтому убыток составит все $546 стоимости опциона. Если мы предположим, что скорость падения была настолько велика, что не оставалось времени для рехеджирования, тогда прибыль по 50 коротким акциям составит 50х60=$3.000, а чистая прибыль будет равна 3.000-546=$2.454. Если цена акции упадет больше, чем на $60, то прибыль будет еще больше. Теперь мы видим, как участники рынка, которые пользовались этой стратегией, смогли получить огромную прибыль во время краха рынка в 1987 году.
B. Взлет рынка
Предположим, что произошла обратная ситуация. Сразу же после начала торга цена акции внезапно поднялась на $60 — до $159. На этом уровне опцион будет настолько глубоко в деньгах, что будет оценен по его внутренней стоимости, а именно в $59, в результате чего прибыль составит 100х(59-5,64)=$5.336. Убыток от короткой позиции будет 50х60=$3.000, вследствие чего чистая прибыль будет равна 5.336-3.000=$2.336. При росте цены более чем на $60, прибыль — увеличивается.
Время от времени такие ситуации действительно возникают. На протяжении ряда лет наблюдалось множество серьезных падений цен. Многократно происходило слияние фирм, что приводило к почти моментальным взлетам цен. Длинная торговля волатильностью всегда приносит прибыль в результате таких огромных подвижек цен. Полученная прибыль зависит от резкости ценовых изменений. При крахе рынка цены на акции не могут опуститься ниже нуля, поэтому возможно посчитать максимальную прибыль ($4.404 в вышеприведенном примере). Теоретически верхнего предела для цены акции не существует, поэтому невозможно определить верхнего предела прибыли. Таким образом, длинная игра волатильностью имеет неограниченный потенциал прибыли, а наряду с фактом наличия ограниченных убытков является очень привлекательной стратегией.