3.1 Опцион колл
Существуют рынки опционов колл на акции, товары, валюту, фондовые индексы, фьючерсы и процентные ставки. Каждый тип опциона оценивается по-разному, но основное ценовое поведение всех опционов колл можно понять, рассмотрев только один вид опциона — опцион на покупку акции, которым и является опцион колл. Поэтому на протяжении всей книги речь будет идти именно о колл опционах.
Определение: Опцион колл на акцию предоставляет право, но не обязательство купить определенное количество акций по определенной цене в или до определенного дня.
Количество акций фиксировано и обычно составляет либо 100 штук, либо 1.000 штук. Цена называется ценой исполнения (exercise price), или ценой страйк (strikeprice), а определенный день называется датой истечения срока (expiry date). Часто акцию, лежащую в основе опциона, называют основным (базовым) инструментом (underlying).
Например, опционы на IBM дают право приобрести 100 штук акций IBM. Существует множество опционов на IBM, но мы рассмотрим только один. В день, когда цена акции составляет, скажем $102, имеется опцион с ценой исполнения $100 со сроком истечения 3 месяца. Оставим на некоторое время вопрос о стоимости этого опциона и перейдем прямо к тому дню, когда истекает срок, минуя тем самым эти три месяца.
- 1. Владелец может "исполнить" опцион и купить акцию по цене исполнения $100. В этом случае сумма, которая требуется для исполнения, выплачивается полностью, а взамен владелец получает 100 акций: владелец потребовал (called) акцию по цене $100, отсюда и термин "опцион колл". Если владелец исполняет опцион, то необходимо заплатить дополнительно 100х100=$10.000. Если цена акции выше, чем цена исполнения $100 на бирже, тогда этот путь самый оптимальный. Если акция торгуется по $104, тогда владелец может продать все 100 акций и получить $4 с каждой акции, что в сумме составит 100х4=$400. Если акция торгуется по $108, тогда окончательная стоимость составит 100х8=$800.
- 2. Владелец может выбрать другой путь: не исполнять опцион. Если акция торгуется по $94 на бирже, тогда понятно, что нет никакого смысла в использовании права на покупку по $ 100. Если акция действительно нужна, то на бирже ее можно купить дешевле. В этой ситуации владелец дает опциону истечь безрезультатно. Этот путь может быть выбран, если цена акции на рынке хоть на сколько-нибудь ниже цены исполнения $100. В этой ситуации опцион вообще не будет иметь какой-либо окончательной стоимости, и мы говорим в таких случаях, что опцион истекает бесполезно.
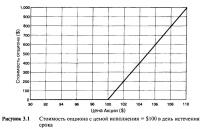
Таблица 3.1 отражает окончательную стоимость опциона колл при различных ценах на акцию. Рисунок 3.1 является графическим изображением окончательной стоимости.
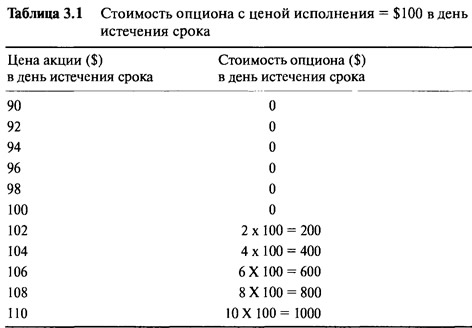
Мы видим, что ситуация очень сходна с тем, что наблюдается в случае с конвертируемой облигацией. Выше определенной цены (цены исполнения), равной 100, наклон прямой линии постоянен: владелец опциона колл предпочитает 100 акций IBM. Ниже цены исполнения наклон равен нулю: владельца в этом случае вообще не интересуют цены, существующие на акции IBM. Единственная разница состоит в том, что ниже определенной цены конвертируемая облигация возвращает единовременно выплачиваемую сумму, а опцион колл ничего не возвращает.
В вышеприведенном примере мы считали стоимость опциона, предполагая, что владелец исполнит его, получит, а затем продаст акцию. На практике, чаще всего, это совсем не обязательно. Существует хорошо функционирующий рынок опционов, и в реальных ситуациях опцион может быть продан по внутренней стоимости. Поэтому, если цена акции была $106, тогда опцион колл с ценой исполнения $100 может быть продан без труда за $600, или $6 за акцию. И обычно нет необходимости прибегать к процедуре истребования акции.
3.2 Терминология опционов
Торгуемые на рынке фондовые опционы имеют три, шесть и девять месяцев жизни и различные цены исполнения. Проходит время, и срок опциона истекает (иногда имея стоимость, а иногда и нет), поэтому биржи выпускают новые опционы.
Опцион колл, чья цена исполнения ниже текущей цены акции, называется опционом "в деньгах" (in-the-money). Опцион колл, чья цена исполнения выше текущей цены акции, называется опционом "без денег" (out-of-the-money). Опцион колл, чья цена исполнения равна, или приблизительно равна текущей цене акции, называется опционом "около денег" (at-the-money). Большинство рынков непрерывно регистрируют опционные выпуски, поэтому существует, по крайней мере, один опцион в деньгах и один опцион без денег для каждого цикла истечения срока (expiry cycle).
В вышеуказанном определении опциона колл выражение "в или до определенного дня" означает, что этот опцион является опционом Американского стиля (American style). Владелец такого опциона может, если пожелает, исполнить свой опцион раньше срока, и ему совсем не обязательно утомлять себя ожиданиями последнего дня. Существуют некоторые опционы, которые могут быть исполнены только в день истечения срока. Такие опционы называются опционами Европейского стиля (European style). Во многих случаях ценовая разница между двумя типами опционов равна нулю или совсем небольшая.
Опционы колл, очевидно, могут быть очень прибыльным инвестированием. В качестве примера рассмотрим ситуацию с акциями IBM, торгуемыми по $102 на рынке: в этом случае трехмесячный опцион колл в деньгах с ценой исполнения $100 может быть оценен примерно $3,50 за акцию. Цены опционов всегда назначаются из расчета некоторой суммы за акцию. Однако каждый опцион на IBM является контрактом на 100 акций, поэтому один опцион будет стоить 100x3,50=$350. В этой книге мы всегда будем говорить о цене опциона из расчета некоторой суммы за акцию. Мы также будем предполагать, что опцион является контрактом на покупку 100 акций. Соответственно стоимость, или цена опциона иногда будет рассматриваться, как $3.50, а иногда — $350. Мы говорим, что этот опцион уже $2 в деньгах, имея в виду, что если его немедленно исполнить, то можно возместить, по крайней мере, разницу между рыночной ценой и ценой исполнения. Эта величина, появляющаяся при нахождении опциона в деньгах, называется внутренней стоимостью (intrinsic value). Разница между внутренней стоимостью и ценой опциона, в этом случае составляющая $3,50-$2,00=$1,50, называется временной стоимостью (time value). Временная стоимость — это деньги, которые спекулянт подвергает риску, если цена акции остается неизменной. Конечно, можно потерять больше временной стоимости, если цена акции упадет.
Эта книга — не учебное пособие по опционным рынкам или опционным стратегиям. На эту тему существует много блестящих работ, написанных простым и доступным языком, поэтому при необходимости читатель всегда может к ним обратиться.
3.3 Вероятность, средние значения, ожидаемые выплаты и справедливая стоимость
Чтобы понять всю сложность оценки производных финансовых инструментов до момента истечения, будет полезно взять на вооружение понятия, связанные с исчислением средних значений и предлагаемую концепцию вероятности. Это можно сделать с помощью простейшей арифметики. Не требуется никаких сложных математических подсчетов.
Представьте, что вы — в казино и играете в кости. Вы бросаете один кубик. Выплата будет равна тому количеству точек, которое окажется на верхней стороне кубика, когда он остановится. Если выпала единица, то вы получаете $1. Если двойка — то $2, и так далее. Максимум, что вы можете выиграть — это $6, и минимум — $1. Вопрос только в том, какую цену назначит казино за эту игру, если речь идет ни о прибыли, ни об убытке? Большинство читателей интуитивно назовут правильную сумму — $3,50, но нам лучше объяснить весь процесс вычисления "справедливой стоимости". Мы называем эту стоимость "справедливой", потому что если вы заплатите больше, то по истечении долгого периода времени вы, вероятнее всего, проиграете, но если заплатите меньше, то вероятнее всего, выиграете. Предположим, что игра повторяется 6.000 раз. Если игральный кубик без повреждений, то за это время одна шестая всех бросков придется на единицу, одна шестая на двойку, одна шестая на тройку и так далее. Таким образом, из 6.000 бросков 1.000 бросков, давших единицу, составят в итоге 1.000x1=$1.000. Точно также 1.000 бросков, давших двойку, составят 1.000х2=$2.000 и так далее. В Таблице 3.2 приведены все расчеты. Мы видим, что после 6.000 игр "ожидается" окончательная выплата, величина которой составляет $21.000. Таким образом, "средняя" выплата будет равна 21.000/6.000=$3,50 за одну игру. Поэтому, если бы мы играли в эту игру 6.000 раз и платили бы каждый раз $3,50 за участие в ней, тогда бы мы (и казино тоже) достигли уровня безубыточности. Если бы наш платеж составил $4 за каждую игру, тогда в среднем мы потеряли бы $0,50 за игру или в итоге: 6.000х0,50=$3,000. Если бы мы платили $3,20, тогда в среднем зарабатывали бы $0,30 за одну игру, что в итоге составило бы 6.000x0,30=$1.800.
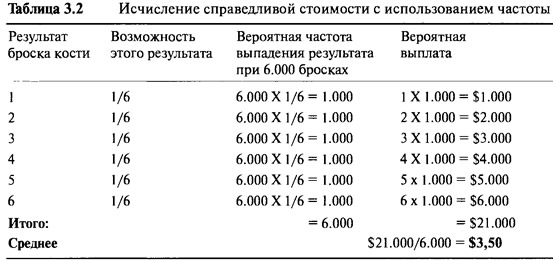
В этом примере мы говорили об игре, продолжительность которой составила 6.000 бросков, потому что 6.000 удобно делится на 6. Также легко можно было бы "сделать" 60.000 бросков или 6 миллионов — результат был бы один и тот же: средняя выплата, а следовательно, справедливая цена составляет $3,50. Математики называют такие "будущие средние значения" или "ожидаемые средние значения" пока что нереализованных чисел ожидаемыми значениями (expected values). Сколько бы раз вы ни играли в эту игру, ожидаемое среднее значение все равно составит $3,50 за игру. Интересно то, что ни один бросок никогда не принесет вам ожидаемой выплаты, — то есть $3,50 никогда не будет оплатой одного броска. Эта цифра появится только как среднее значение за чрезвычайно продолжительный период времени.
В данном случае, учитывая, что игральный кубик не поврежден, все вероятностные результаты являются равновозможными. Такое распределение результатов называется нормальным (uniform). При таком нормальном распределении существует более легкий способ вычисления ожидаемой, или по-иному, справедливой стоимости. Чем бросать кости 6.000 раз, лучше представим, что кубик кидают 6 раз. Так как результаты равновозможны, то предположим, что каждое число выпадает только один раз. Таким образом, единица предполагает выплату в $ 1, двойка в $2 и так далее. Это отражено в Таблице 3.3. При шести бросках общая выплата составляет $21. А $21 за шесть бросков означает 21/6=$3,50 за бросок.

Теперь представим себе эту игру по-другому. На этот раз при выпадении единицы или двойки выплачиваться ничего не будет. Какова тогда будет эта новая справедливая стоимость? Так как распределение все еще нормальное, то мы можем использовать простейший способ, показанный в Таблице 3.4.

Итак, в новой игре более низкое среднее значение за тот же длительный период — $3,00 за игру. Это неудивительно, так как два из шести бросков (единица и двойка) не требуют выплаты. Тип выплаты, который представлен в Таблице 3.4, напоминает что-то вроде опциона колл в день истечения его срока. Некоторые результаты являются нулевыми, а остальные — линейно увеличиваются.
Теперь мы используем этот тип доказательства, чтобы понять, каким образом опционы колл оцениваются до наступления окончания срока их обращения.
3.4 Справедливая стоимость опциона колл
Теперь перейдем к методу вычисления цены опциона колл до наступления срока его истечения. Он строится на предположении, которое на первый взгляд кажется нереальным. Выработанный на основе концепции вероятности, представленной ранее, этот метод хорош тем, что не требует сложных математических расчетов. Метод также предоставляет в высшей степени реальный профиль опционной цены.
Опцион около денег
Рассмотрим покупку опциона с ценой исполнения $100, который истекает через три месяца. Сегодня цена акции $100, поэтому — это опцион около денег. Сколько следует заплатить за этот опцион? Мы знаем, что если цена акции поднимется до $105, то опцион будет стоить $5. Однако если цена акции опустится до $95, то мы потеряем все свои инвестиции. Для простоты предположим, что в день истечения срока цена акции может подняться или опуститься только на $5. Более того, предположим, что цена акции может быть только целым числом, то есть одним из следующих 11 чисел: $95, $96, $97, $98, $99, $100, $101, $102, $103, $104 или $105. Также предположим, что каждая из этих 11 цен равновероятна. Соответственно, в таких случаях цены опциона колл в день срока истечения составили бы $0, $0, $0, $0, $0, $0, $1, $2, $3, $4 и $5. В Таблице 3.5 перечислены все возможные значения.
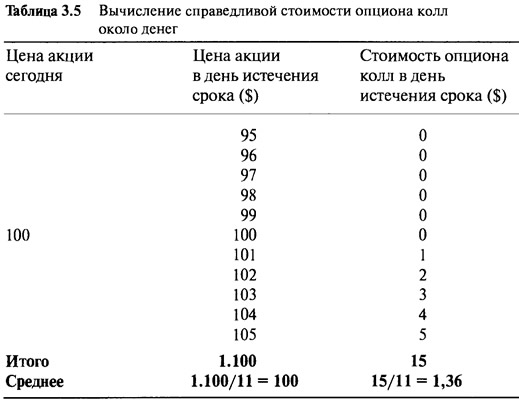
Ситуация напоминает игру в кости, за исключением того, что в данном случае существует 11 возможных результатов. Представьте теперь, что разыгрываются две "игры". В первой игре инвестор каждый раз покупает акцию по $100, ждет три месяца, а затем продает. Иногда (один случай из одиннадцати) окончательная цена акции составляет $105, иногда $104 и т.д. Если инвестор играет в эту игру достаточно часто, то за долгий период времени среднее значение окончательной цены составит $100. Этот пример был приведен специально для того, чтобы показать, что никакого отклонения в цене опциона нет.
В другой игре инвестор повторно покупает опцион (по цене, пока неизвестной) и ждет три месяца до дня истечения срока. Иногда (один случай из одиннадцати) окончательная выплата составляет $5, иногда $4 и т.д., но чаще всего (шесть раз из одиннадцати) опцион обесценивается, истекая бесполезно. Так как каждый из результатов равновозможен, то легко посчитать среднюю выплату по опциону. Таблица 3.5 показывает, что средняя выплата по нему равна $1,36. Для того чтобы инвестор опциона, так же как и инвестирующий в акции, достиг уровня безубыточности, он должен заплатить $1,36 за участие в игре. Если он заплатит больше $1,36, то проиграет за длительный период, а если он заплатит меньше, то выиграет. Справедливая стоимость опциона при этих простых допущениях составляет $1,36.
Прежде, чем мы продолжим, стоит еще раз обратиться к Таблице 3.5. При определении средней цены акции в день истечения срока нет необходимости утруждать себя сложением всех значений: $95+$96+...+$105, чтобы получить окончательное значение $1.100, а потом делить его на 11, чтобы получить $100. Гораздо более простой метод — это учесть, что распределение цен абсолютно симметрично относительно $100, что несомненно, и является средней ценой. При симметричном распределении середина (которую еще называют медианой) всегда равна среднему значению. Но это совсем не так в отношении распределения цены опциона при наступлении срока его обращения. Цены опционов при наступлении срока асимметричны. Шесть стоимостей из одиннадцати равны нулю, а остальные линейно увеличиваются. Асимметрия является ключевым моментом в опционном контракте. Тот факт, что владелец имеет право, но не обязательство на приобретение акций, означает возможность избежать проигрышной ситуации при падении цены акции.
Опционы в деньгах
Давайте предположим, что цена интересующей нас акции внезапно поднялась на $1, достигнув $101. Какова будет стоимость трехмесячного опциона колл с ценой страйк $100? Теперь у нас уже другая ситуация. При цене акции $101 необходимо пересмотреть будущие вероятностные результаты. Для упрощения давайте предположим, что распределение остается асимметричным относительно новой цены и, что цены в день истечения срока опять интегрально поднимаются или опускаются на $5 от отметки $101. Соответственно, окончательные цены акции устанавливаются следующим образом: $96, $97, ..., $105, $106. Таблица 3.6 отражает эту новую ситуацию.
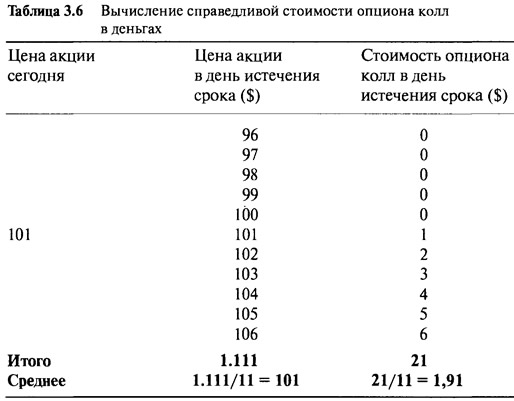
Справедливая стоимость опциона теперь $1,91. Она на $0,55 больше цены $1,36, когда акция стоила $100, и это является вполне обоснованным. Цена должна быть выше, так как выше вероятность того, что опцион в день истечения срока будет чего-то стоить. Сейчас вместо шести мы имеем всего пять ситуаций, при которых опцион может обесцениться. Максимальная выплата тоже увеличилась: $6 вместо $5.
До того, как продолжить вычисления справедливой стоимости, рассмотрим еще раз эти ситуации. При цене акции $100 стоимость опциона составляет $1,36. При увеличении цены акции до $101 опционная премия увеличилась до $1,91. Вполне наглядна спекулятивная привлекательность опциона по сравнению с акциями. Что будет более прибыльным: покупка акции по $100 и ее продажа по $101 или покупка опциона по $1,36 и его продажа по $1,91? В первом случае инвестиция обернется прибылью в 1%, тогда как в последнем в 40%. Однако заметьте, что если с точки зрения процентного изменения, стоимость опциона увеличилась больше, чем акция, то в абсолютном отношении цена опциона поднялась лишь на $0,55 по сравнению с ростом цены акции на $1, и это является наиболее важным наблюдением.
Опционы вне денег
Давайте предположим, что цена интересующей нас акции не поднялась, а упала на $1 до $99. Опцион колл с ценой исполнения $100 теперь вне денег. По той же самой логике в Таблице 3.7 представлены вычисления новой справедливой стоимости, равной $0,91, которая является вполне обоснованной, так как возможные результаты для игрока ниже, чем в тот момент, когда цена акции составляла $100.
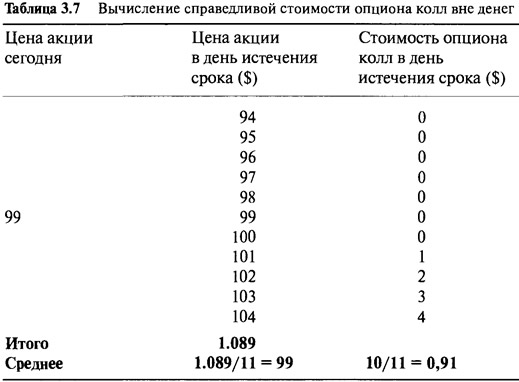
Мы можем использовать этот способ для расчета любых цен акций, чтобы получить полную картину того, как изменяется справедливая стоимость опциона колл. Читатель может сам произвести эти расчеты для цен $93, $94,..., $106 и $107. Результаты приведены в Таблице 3.8.
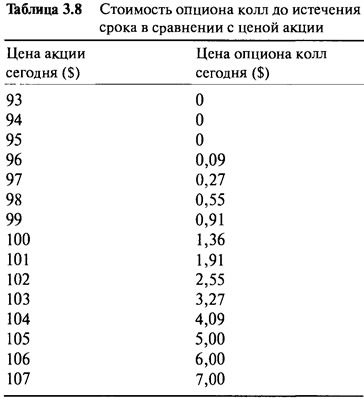
На Рисунке 3.2 изображена кривая цены опциона относительно линии цены акции. Обратите внимание на кривую цены опциона. Именно так на самом деле изменяются цены опционов колл. Хотя мы использовали почти нереальные предположения о распределении цены акции, полученная кривая цены сходна по значениям с исследуемыми опционами колл.
- 1. Опционы, находящиеся далеко без денег оцениваются нулем. При цене акции ниже или при $95 мы знаем, что опционы никогда не будут чего-либо стоить из-за того, что цена акции может увеличиться максимум на $5. При таких низких ценах наклон кривой цены также будет равен нулю. В действительности мы обнаруживаем, что это так и есть. Цена опционов, находящихся далеко без денег, равна или почти равна нулю, и они совсем не чувствительны к изменениям цены акции.
- 2. Опционы, находящиеся далеко в деньгах, оцениваются внутренней стоимостью. Заметьте, что опцион уже не оценивается временной стоимостью при высоких ценах акций. Скажем, при цене акции $105 цена опциона составляет $5. Таким образом, при таких высоких ценах чувствительность опциона колл очень высока. При значениях выше $105 чувствительность равна 100%.
- 3. Изменение от низкой цены к высокой цене является постепенным и нелинейным. Переход от низкой стоимости $0 к высокой стоимости в $7 является плавным. Обращаясь к оценке наклона кривой, можно увидеть, что она постепенно увеличивается от 0 до 1. На $93 наклон равен 0, на $100 — 0,5 и на $107 наклон составляет 1.
Все эти особенности опционов колл проявляются также и в реальной жизни.
3.5 Нелинейность цен опциона колл и процесс усреднения
Цифры, представленные в Таблице 3.8 и используемые для составления графика, который дан на Рисунке 3.2, являются результатом простой арифметики. Каждое среднее значение, или справедливая стоимость, определены процессом усреднения 11 цифр. Рассмотрим процесс усреднения заново. Начнем с того, что текущая цена акции равна $100, и среднее значение в Таблице 3.5 вычисляется следующим образом:
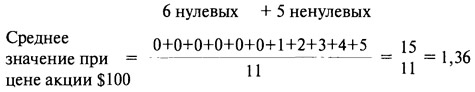
Далее в ситуации, где цена акции равна $101, новое среднее значение считается так:
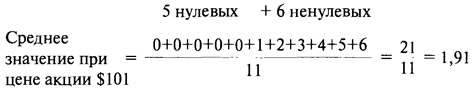
В обеих дробях в числителе сумма из 11 чисел. Разница между первой и второй суммой состоит в том, что появилось число 6 и пропал ноль. Это означает, что сумма увеличилась на 6, или — среднее значение увеличилось на 6/11, то есть на 0,55, составив 1,91.
Ищем следующее среднее значение, принимая во внимание, что цена акции составляет уже $102:
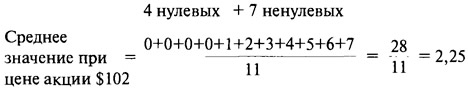
Разница между второй и третьей суммой — это появившаяся 7 и пропавший ноль. Это означает, что сумма увеличилась еще на 7 или что среднее значение увеличилось на 7/11, или на 0,64, составив 2,55.
Мы могли бы продолжить этот процесс, последовательно рассматривая растущие цены. Каждый раз сумма определялась бы отбрасыванием одного нуля и прибавлением одной цифры. Прибавляемая цифра тоже увеличивалась бы на одну единицу. В результате сумма увеличивается, причем нелинейным образом. При каждом шаге сумма увеличивалась бы еще на одну единицу. Так как сумма увеличивается по строго возрастающему пути, то и результирующее среднее значение увеличивается также. Именно поэтому мы имеем кривую линию. Причина этого — нули. В Таблице 3.9 расписан весь процесс усреднения.
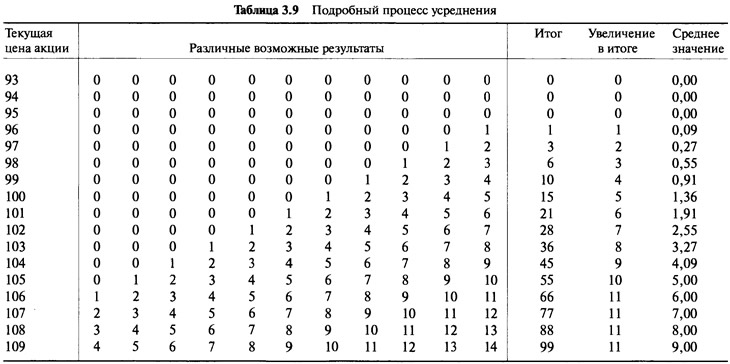
Заметьте, что как только текущая цена акции поднимается выше уровня в $105, суммы (а следовательно, и среднее значение) начинают вести себя по-разному. После того, как достигается цена $105, нулей больше не появляется. Выше отметки $105 каждая новая сумма продолжает увеличиваться за счет добавляемой цифры, но цифра, которая вычитается из суммы, уже не ноль. Каждая исключаемая цифра всегда на 11 единиц меньше добавляемой цифры. Соответственно, сумма увеличивается на постоянное число, равное 11, поэтому среднее значение увеличивается на 1. Выше цены $105 степень увеличения средней величины остается постоянной. На графике строго возрастающая кривая выравнивается в прямую линию.
При рассмотрении цен на более низких уровнях ситуация прямо противоположна. Количество нулей, входящих в состав суммы, увеличивается до тех пор, пока все цифры не заменятся нулями. Ниже цены $96 за акцию суммы, а следовательно, и средние значения постоянно находятся на нуле.
Особенности, которые демонстрирует справедливая стоимость опциона, являются прямым результатом процесса усреднения. Когда возможные результаты имеют асимметричное распределение, средние значения вырисовывают кривую линию. Все результаты, полученные нами выше, были равновозможны, поэтому расчеты оказались несложными. Однако можно доказать, что, какой бы тип распределения ни имели различные вероятностные результаты, асимметрия всегда будет вычерчивать кривую ценового профиля с очень похожими характеристиками. Это означает возможность графически изобразить более реалистичное распределение цены акции, а также получить более точное описание профиля цены опциона.
3.6 Справедливая стоимость опционов колл с дальней датой истечения
В вышеприведенном примере мы предполагали, что цена акции при наступлении срока истечения может иметь одно из 11 различных значений вокруг текущей цены акции, а опцион имел три месяца до истечения срока. Теперь мы задаем вопрос относительно определения цены шестимесячного опциона колл на ту же акцию. Очевидно, что шестимесячный опцион должен стоить больше, чем трехмесячный опцион, но как нам определить его стоимость, используя все тот же простой метод? Ответ прост. Мы снимем ограничения относительно колебания цены акции на $5 и позволим цене увеличиваться и уменьшаться на $8. Таким образом, мы будем иметь 17 возможных окончательных цен акций: $92, $93, ..., $107, $108 с соответствующими ценами опциона: $0, $0, ..., $7, $8. Читателю остается самому пройти весь путь, описанный выше, и доказать, что справедливая стоимость теперь составляет $2,12. Вычисленные тем же способом справедливые стоимости шестимесячного опциона при различных ценовых значениях акции приведены в Таблице 3.10 и на Рисунке 3.3.
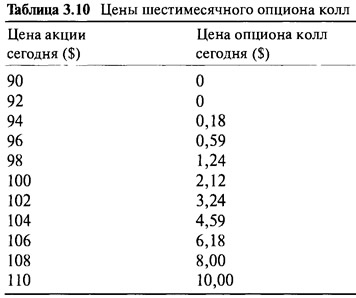
Для сравнения, кривая трехмесячного опциона тоже проведена на Рисунке 3.3. Шестимесячный опцион имеет те же самые особенности, что и трехмесячный опцион. В большинстве случаев при одинаковой цене акции цена шестимесячного опциона выше, чем трехмесячного. И это вполне понятно. Два опциона имеют одинаковую стоимость лишь при очень низких и очень высоких ценах на акции. И это целиком и полностью подтверждается практикой.
3.7 Представление более реалистичных предположений о виде распределения
В самом начале мы утверждали, что предположение о нормальном распределении цен акции в какой-то момент в будущем нереально. Если сегодня акция оценивается в $100, то на самом деле мы не можем говорить о равных возможностях цен в $95, $96,..., $105 в будущем трехмесячном периоде. Многие дадут больше шансов за то, что текущая цена акции в будущем не изменится. До тех пор, пока не произойдет какое-либо экстраординарное событие, будет считаться, что цена акции через три месяца будет примерно такой же, как и сегодня. Также нереально и предположение о том, что цена акции будет падать или расти максимум на $5.
Существует множество математических моделей, описывающих распределение цен акций, и все они с большой долей вероятности определяют текущие цены акций, допуская экстремальные движения. Большинство стандартных моделей предполагает логнормальное распределение (lognormal distribution) для описания процентных изменений. Нет необходимости углубляться в математические сложности этого распределения, однако следует отметить, что результаты многих эмпирических исследований финансовых ценовых рядов получены на основании именно логнормального распределения. В 1973 году Майрон Шоулз и Фишер Блэк1 решили проблему вычисления ожидаемого значения цены опциона колл, взяв за основу логнормальное распределение. Широкое применение метода Блэка и Шоулза привело к тому, что он стал фактически общепринятой "истинной" ценовой моделью. Читатель, интересующийся происхождением модели Блэка и Шоулза, а также ее подробным описанием, может обратиться к блестяще написанным на эту тему математическим работам. Модель настолько широко применяется, что большинство служб финансовой информации, такие как Bloomberg и Reuters, свободно производят оценку опционов, используя методы Блэка и Шоулза. Этот подход настолько широко распространен на валютных рынках, что профессионалы в действительности предпочитают использовать параметры модели, нежели цены. На дискете, которая прилагается к этой книге, вы найдете исчерпывающую информацию об этой модели2.
Так в чем же состоит эффективность применения этого другого распределения, отличающегося от нашего "наивного" нормального распределения? Логнормальное распределение придает большую значимость текущей цене акции и меньшую значимость будущим ценам. Допущение меньшей вероятности экстремумов в распределении существенно уменьшает шансы возникновения большой стоимости опциона при истечении его срока и влияет на уменьшение ожидаемой стоимости. Но это, однако, компенсируется тем, что логнормальное распределение допускает вероятность очень экстремальных движений. На Рисунке 3.4 представлены кривые цен трехмесячного опциона колл, полученные при использовании "корректного" логнормального распределения, а именно модели Блэка-Шоулза, и нашего "наивного" нормального распределения.
Обратите внимание на значительное сходство двух ценовых кривых. Обе они приближаются к горизонтальной линии (нулевой цене) и обе сближаются с линией внутренней стоимости. Кривые немного отличаются в экстремумах. Кривая Блэка-Шоулза (т.е. логнормальная) выводится из сложной системы уравнений, в то время как "наивная" кривая является результатом совсем несложной арифметики. Обе кривые демонстрируют асимметричность ценовых профилей к дате истечения, а возникшее расхождение можно рассматривать как вероятности различных исходов. Целью этой главы было доказать с помощью простых аргументов, что причины, лежащие в основе наблюдаемой нелинейности цен опционов, не зависят от используемого способа доказательства. Нет необходимости детально разбираться в поведении кривой ценового профиля. Скорее, нужно понять, почему эта кривая существует вообще.
3.8 Процентная ставка и учет дивидендов
На протяжении всей главы мы не придавали значения влиянию процентных ставок и дивидендов на опционы колл, обращающиеся на акции. В действительности, опционы на акции (в особенности опционы глубоко в деньгах) находятся под влиянием процентных ставок. При прочих равных условиях, если процентная ставка увеличивается, то опцион колл на акцию растет в цене. Также при прочих равных условиях, если на базовую акцию выплачиваются дивиденды, то опционы колл дешевеют.
Мы не намерены углубляться во все сложности, а только приведем несколько графических примеров. На Рисунке 3.5 мы показываем кривые линии цены для трехмесячных опционов на акцию, предполагая различные процентные ставки и используя более подходящую для этого модель Блэка-Шоулза. Заметьте, что опционы в деньгах сильнее поддаются влиянию процентных ставок, нежели опционы без денег. Процентные ставки оказывают влияние путем подъема линейной части линии цены над линией внутренней стоимости. Однако цель этой книги не в том, чтобы изучать влияние процентных ставок, а в том, чтобы обратить внимание читателя на то, что изгиб все еще имеется, но он немного смещен.
3.9 Экспозиция по акции опционов колл и дельта
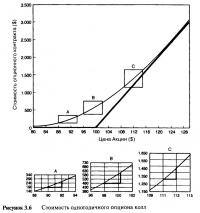
Теперь нам нужно подробно рассмотреть, каким образом меняется экспозиция по акции опциона колл. Весьма удобно, как для этой, так и для многих других экспозиций, рассматривать более долгосрочный опцион, поэтому Рисунок 3.6 показывает кривую цены одногодичного опциона колл с ценой исполнения $100. Для упрощения предположим, что мы имеем дело с ситуацией при нулевой процентной ставке, а опцион ведет себя полностью в соответствии с моделью Блэка-Шоулза. Этот опцион будет использоваться в качестве образца на протяжении всей четвертой главы, а подробный перечень цен будет представлен ниже. Однако здесь особое внимание нужно обратить на три точки кривой "А", "В" и "С".
Цены опциона, стоимость опционного контракта и выявленные значения эквивалентности акции относительно этих точек приведены в Таблице 3.11.
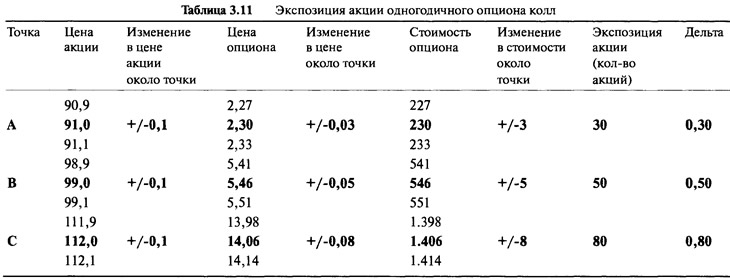
Точка "А": с опционом без денег
В точке "А' при цене акции $91 опцион оценивается в $2,30, поэтому один опционный контракт будет стоить 100х$2,30=$230. Если цена акции увеличивается или уменьшается на очень маленькую сумму, скажем, на 10 центов, или $0,10, то мы видим, что стоимость опциона увеличивается или уменьшается на 3 цента ($0,03), а стоимость контракта увеличивается или уменьшается на $3. Сколько базовых акций нам понадобится, чтобы выразить это изменение в стоимости? Ответ: 30 акций. Умножая 30 акций на 10 центов, получим 300 центов или $3. Во второй главе мы доказали, что экспозиция по акции какой-либо инвестиции эквивалентна наклону стоимости, или линии прибыли и убытка. Линия стоимости здесь не прямая, а изогнутая. Поэтому наклон, а следовательно, и экспозиция по акции, постоянно меняются. Для небольших изменений цены акции мы можем аппроксимировать наклон кривой, нарисовав касательную и приблизительно посчитав ее наклон. Вставка на Рисунке 3.6 показывает, что наклон кривой в точке "А" взят из маленького треугольника, нарисованного под касательной. В точке "А" наклон равен 30, что неудивительно. Хотя рассматриваемый опцион может исполниться на 100 акций (при наступлении срока), в точке "А" он ведет себя так, будто исполнение может произойти только на 30 акций. Стоимость опциона меняется так, будто это портфель, состоящий только из части акции, действительно лежащих в покрытии. Эта часть составляет: 30/100=0,30. Эта часть называется дельтой (delta) опциона и является одним из наиболее чувствительных показателей измерений опциона.
Вспомните портфель "черный ящик", о котором шла речь во второй главе. Вспомните, что содержимое портфеля не было раскрыто, но был представлен профиль цены. В различных точках портфель имел различные экспозиции определенной акции. Также еще экспозиция акции никоим образом не была связана со стоимостью портфеля. Похожую ситуацию мы наблюдаем и в точке "А". Если инвестор купит один опционный контракт в точке 'А', когда цена акции составляет $91, тогда он заплатит за него всего $230. Как только цена акции начнет меняться, он обнаружит, что инвестировал во что-то, что ведет себя так, будто содержит в себе 30 акций. Инвестор обычной акции должен будет заплатить $2.730, чтобы получить ту же самую экспозицию, в то время как инвестор опциона должен будет заплатить только $230. Мы говорим, что передача, или действие рычага (gearing or leverage) составляет 2.730/230=12 (приблизительно). Аналогично случаю с портфелем "черный ящик", как только цена акции начинает движение, экспозиция также начинает изменяться.
Точка "В": с опционом в состоянии близко у денег
В точке "В" цена акции составляет $99,00 и опцион почти около денег. Цена опциона увеличилась до $5,46, поэтому один контракт будет стоить $546. Также мы видим, что наклон кривой и экспозиция по акции увеличились до 50 акций. В точке "В" опцион ведет себя так, будто владелец имеет 50 акций. Здесь дельта составляет 50/100=0,50. В точке "А" опцион имел экспозицию в 30 акций, а в точке "В" это значение увеличилось до 50 акций, причем владелец опциона ничего для этого не делал. Это и есть привлекательная сторона опционов колл. Действительная экспозиция по акции, которая лежит в основе, увеличивается по мере роста цены акции. Это как если бы владелец покупал больше акций по мере увеличения их стоимости.
Точка "С": с опционом в деньгах
В точке "С" кривая намного круче. Опцион ведет себя так, будто содержит 80 акций, поэтому дельта теперь равна 0,80. При такой высокой цене акции стоимость опциона начинает сильнее реагировать на изменения. В точке "С" опцион охватывает 80% движений цены акции.
Выше точки "С"
Легко увидеть, что по мере продолжения роста цены акции стоимость опциона тоже продолжала расти. Как только цена акции поднялась выше точки "С", экспозиция, или наклон, тоже поднялась, но, в конце концов, приблизилась к постоянному максимальному значению 100. При очень высоких ценах акции дельта сближается с константой, которая равна 1,0. После определенной точки (в данном случае выше $ 140) изменение в стоимости опциона в точности повторяет изменение в стоимости 100 акций.
Ниже точки "А"
Если бы произошло обратное и цена акции упала, то стоимость опциона, равно как и экспозиция акции, тоже бы упали. Если цена падает достаточно низко, то дельта, в конце концов, снижается до нуля.
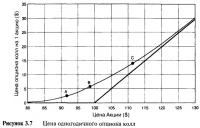
3.10 Дельта как наклон
Ранее дельта была определена как соотношение между экспозицией (выявленного значения эквивалентности) по акции опциона и количеством акций, которое могло бы быть исполнено по опциону. В точке "А" дельта составляла 0,30, в точке "В" дельта была 0,50 и так далее. Однако можно подумать, что дельта это и есть наклон. Еще раз обратитесь к Таблице 3.11 и посмотрите не на изменение стоимости контракта, а на изменения в ценах с точки зрения цены за одну акцию. Вокруг точки 'А', если цена акции двигается по 10 центов, цена опциона сдвигается на 3 цента. Коэффициент этих ценовых движений составляет 3/10=0,30, которая есть дельта. В точке "В" коэффициент ценовых движений составляет 5/10=0,50, то есть дельта. Таким образом, мы можем сделать заключение, что дельта опциона также является измерением чувствительности цены. Дельта есть скорость изменения цены опциона по отношению к изменению цены акции, потому и должна быть наклоном цены опциона в сравнении с кривой цены акции, показанной на Рисунке 3.7. Несложно увидеть, что наклон кривой цены равен приблизительно нулю при низких ценах акций и приблизительно единице при высоких ценах акций.
3.11 Профиль дельты
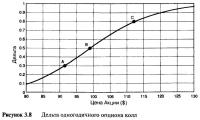
Для человеческого глаза профиль цены на Рисунке 3.7 кажется очень ровным. Переход от низко оцениваемых опционов к высоко оцениваемым опционам постепенный. Мы знаем, почему линия является кривой — из-за изгиба, или асимметрии, которая возникает при наступлении срока истечения. Но как насчет наклона (т.е. дельты) кривой? Таким ли однородным является переход от нуля к единице? Дельту опциона возможно рассчитать при каждом ценовом уровне акции. Дельта опциона также является инструментом модели Блэка-Шоулза и наряду с ценами опционов, большинство информационных служб свободно предоставляют расчеты значений дельты. На Рисунке 3.8 изображена кривая дельты рассматриваемого опциона, построенная по точкам различных уровней цены акции.
Точки "А", "В" и "С" также отмечены на Рисунке 3.8. Обратите внимание, что переход дельты от значений, близких к нулю, до величин, приближающихся к единице, неравномерен. Скорость изменения дельты (наклон наклона) не является постоянной величиной. При низких и высоких ценах дельта увеличивается с меньшей скоростью, нежели при ценах, близких к цене исполнения ($100). Но это не сразу становится очевидным при изучении исходной кривой линии цены, которая дана на Рисунке 3.7. Особенность неравномерного изменения дельты типична для всех опционов и будет подробней описана в последующих главах.
3.12 Резюме
В этом разделе мы доказали, что цена опциона колл до наступления срока представляет собой кривую. Изгиб возникает из-за неопределенности стоимости акции при наступлении срока. Мы достоверно знаем, сколько будет стоить опцион при наступлении срока, но мы не знаем, какова будет цена акции. С помощью простых доказательств, построенных на вероятностных предположениях и несложной арифметике, можно добиться частично искривленной линии. Сам факт того, что цена искривлена, свидетельствует об изменении экспозиции по акции вместе с ценовыми колебаниями акции. Покупка и владение опционом колл — это почти то же самое, что покупка инвестиции, включающей в себя определенную часть (долю) акций. Доля рассматривается как дельта и как наклон кривой линии цены. Опционы колл без денег имеют низкие значения дельты и, соответственно, не слишком реагируют на цену базовой акции. Опционы колл в деньгах имеют более высокие величины дельты, и они намного чувствительней к изменениям цены акции.
Дельта, а следовательно, и экспозиция по акции изменяются вместе с ценой акции. Менеджер фонда, владеющий опционами колл, базовые акции которых увеличиваются в цене, по сути, покупает больше акций на росте цены. Руководитель фонда, владеющий опционами колл, базовые акции которых уменьшаются в цене, по сути, распродает акции при падении цены. Еще раз подчеркнем важность понимания того, что цена, заплаченная за опцион колл, не является экспозицией по акции. Возможно иметь два опциона: один оценивается в 5 (при трех днях до наступления срока), а другой в 20 (при шести месяцах до наступления срока), и при этом опцион более низкой стоимости будет иметь гораздо более высокую экспозицию по акции.
Примечания
1. Myron Scholes, Fisher Black.
2. В английском издании. Заинтересованные читатели могут получить от российского издателя "Аналитика+" по адресу в Сети: www.analitika.ru/connolly.