2.1 Скорость изменения и наклон прямых линий
В этом разделе мы будем изучать и измерять взаимосвязь, существующую между совокупностями переменных. Эта взаимосвязь является искусственной и отображается тремя способами: (1) в форме таблицы, (2) графически, (3) используя измерение скорости изменения. Каждый случай мы рассматриваем относительно двух воображаемых переменных: "X" и "Y'. И в каждом примере представляем, что "X" "толкает" "Y", то есть "Y' зависит исключительно от "X", а "X" зависит от воздействия извне. Мы будем определять взаимосвязь, существующую между "Y' и "X", в том числе саму скорость, с которой "Y' меняется по отношению к "X". Это, в конце концов, приведет к реальным ситуациям, в которых "X" является ценой акции, а У — стоимостью портфеля, содержащего акцию и производную ценную бумагу.
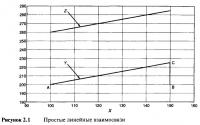
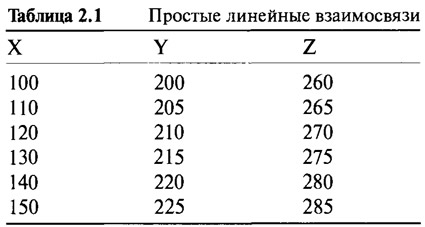
Вначале изучите Таблицу 2.1, в которой приведен список шести установленных значений "X" и "Y". Очевидно, что связь между "X" и "У абсолютна. Если рассматривать, как увеличивается значение "X": 100, 110, 120..., — можно увидеть, как увеличивается значение "Y": 200, 205, 210... Каждое изменение У на 5 единиц явилось "следствием" изменения на 10 единиц значения "X". Рисунок 2.1 отражает ситуацию в графическом виде.
Соединение шести точек, чтобы провести прямую линию, является общепринятым способом, целью чего является показать связь между двумя переменными. Математики, по очевидным причинам, называют подобную взаимозависимость линейной (linear) взаимосвязью. Особенность линейных, или по-другому — прямолинейных взаимосвязей заключается в том, что они могут быть легко охарактеризованы одним простым показателем: отклонением или наклоном линии. Нарисуйте любой прямоугольный треугольник под или над прямой линией: наклон будет характеризовать пропорцию, определяющую соотношение между вертикальной и горизонтальной сторонами. На Рисунке 2.1 при использовании треугольника "ABC" пропорция составила 1 к 2. Наклоны, как правило, выражаются в виде коэффициентов соотношения или процентов, и, таким образом, наклон этой линейной взаимосвязи составляет:
Конечно, этот ответ был очевиден, как следовало из Таблицы 2.1. Так как "X" увеличивается на 10, то "Y' увеличивается на 5. Если бы "X" увеличился на 5, то "Y' увеличился бы на 2,5. Если бы "X" увеличился на 1, то "Y' увеличился бы на 0,5. Короче говоря, скорость изменения "Y' по отношению к "X" равна 0,5, или 50%.
Таблица 2.1 также показывает значения третьей переменной "Z". По мере того, как "X" увеличивается от 100 к 110, к 120 и т.д., "Z" увеличивается от 260 к 265, к 270 и т.д. Переменная "Z" стартует с другого уровня по отношению к "Y', но имеет точно такую же взаимосвязь с "X", то есть скорость изменения тоже равна 0,50. Графически это выглядит, как несколько параллельных линий. На Рисунке 2.1 мы видим, что наклоны обеих линий, несомненно, тождественны и равны 0,50. Способность обеих переменных к реагированию на изменения значений "X" одинакова. Важно понять, что действительное значение или уровень переменной, такой как "X" или "Z", зачастую не имеет значения. Скорость изменения значения по отношению к "X" — вот что действительно важно.
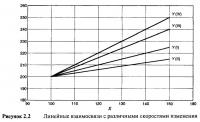
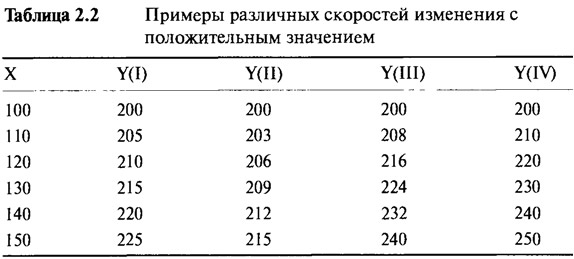
Рассмотрим Таблицу 2.2, в которой приведен перечень четырех воображаемых линейных взаимосвязей Y(I), Y(II), Y(III), Y(IV). Соответствующее графическое изображение дано на Рисунке 2.2. Сгруппированные числа и прямые линии, чьи наклоны различны, отражают тот факт, что взаимосвязи имеют различные степени изменения скорости. Взаимосвязь (I) подобна той, которая была рассмотрена выше, то есть "Y1 увеличивается со скоростью 0,50 по отношению к "X". Что касается взаимосвязей (II), (III) и (IV), то скорости изменения равны 0,30, 0,80 и 1,00 соответственно. Более высокие скорости изменения представлены прямыми с более крутыми углами наклона.

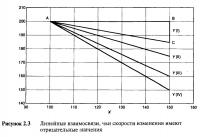
И, наконец, рассмотрим Таблицу 2.3 и Рисунок 2.3. Эти примеры показывают ситуации, в которых по мере того, как "X" увеличивается шажками по 10 единиц, шаги увеличения "Y' представляют собой разные значения. Здесь применяется тот же самый принцип измерения скорости изменения, за исключением того, что если направление изменения "У противоположно направлению изменения "X", то мы определяем наклон и скорость изменения как отрицательные величины. Итак, о взаимосвязи (I), в которой У увеличивается на 3 единицы по мере того, как "X" увеличивается на 10 единиц, можно сказать, что величина наклона, или скорости изменения, равна 0,30. Графически это выглядит так же, за исключением того, что прямоугольный треугольник теперь уже нарисован основанием вверх, а длина вертикальной стороны ассоциируется со знаком минус. Основываясь на значениях Таблицы 2.3, мы можем вычислить наклон линии (I) из треугольника "ABC":
Обратите внимание на то, что величина наклона, помимо всего прочего, определяет еще и крутизну. Линия (IV) имеет наклон "—1", или "—100%", и отражает взаимосвязь с максимальной скоростью изменения, хотя и в перевернутом смысле.
2.2 Длинные и короткие позиции
Несмотря на то, что эти термины уже упоминались ранее, будет полезно более подробно остановиться на определениях лонг (длинной) и шорт (короткой) позиций. Наиболее простой позицией считается лонг. Длинная позиция — это позиция, которая оказывается прибыльной, когда цена актива возрастает. Многие используют такое понятие, как находиться в длинной позиции — то есть купить что-либо в надежде на то, что цена поднимется, а потом продать. Прибыль возникает из разницы между ценой покупки и ценой продажи. Конечно же, если цена упадет, то вы останетесь с отрицательной прибылью, то есть — с убытком. Это простое понятие, если речь идет о покупке акций либо определенного количества товара, или даже некоторой суммы иностранной валюты. Более сложным понятием является нахождение в длинной позиции по фьючерсному контракту. Хотя принцип один и тот же: когда вы покупаете фьючерсный контракт, то связываете себя договором, по которому возникает обязательство по длинной позиции. И, на самом деле, совсем неважно, каким инструментом является фьючерсный контракт и на какой актив он обращается. Для вас важен только рост цены, чтобы иметь возможность продать его позже с выгодой для себя.
Такое понятие, как "открыть короткую позицию" непосвященного человека может просто сбить с толку. На языке рынка это звучит, как "продавать в короткую". Но как можно продать то, чего не имеешь? Забудем на минутку об этом и просто скажем, что открытие короткой позиции принесет прибыль в том случае, если цена снизится, и убыток, если она поднимется. В отношении фьючерсных контрактов короткая позиция - вещь более простая в понимании, если не принимать во внимание лежащий в основе фьючерса базовый инструмент. Открытие короткой позиции просто означает заключение договора, который гарантирует прибыль, если цена упадет, и убыток, если цена поднимется. Короткая позиция закрывается сделкой на покупку. Если цена открытия (продажи) выше цены закрытия (покупки), то можно говорить о прибыли. Это то же самое, что купить что-либо по низкой цене, а затем продать по более высокой, только в обратном порядке. При низкой цене покупки и высокой цене продажи получается прибыль. То, что сделки исполняются в обратном временном порядке, действительно немного противоречит здравому смыслу, так как ничего не переходит из рук в руки, и только лишь контракты определяют возникающие между сторонами обязательства по сделке.
Нахождение в короткой позиции чего-либо реального, например акции, может оказаться гораздо более сложным делом. Обычно используется технический прием, известный как заимствование (borrowing) акции. Для объяснения этого процесса необходимо рассмотреть следующий пример. Определенная акция торгуется на рынке по $100, а кто-то полагает, что ее цена в ближайшем будущем значительно упадет. Этот кто-то, открывающий короткую позицию, назовем его г-ном "А", знаком с руководителем фонда г-ном "ХМ", у которого акция находится в длинной позиции, и эта позиция, скорее всего, останется неизменной, даже если его предположения о падении цены окажутся верными. Г-н "А" обращается к г-ну "ХМ" с просьбой одолжить ему акцию на определенный период времени. Г-н "ХМ" соглашается на отплату залогом (депозитом), величина которого равна цене акции, то есть $100. Г-н "А" отдает в залог $100 г-ну "ХМ" и физически получает акцию, которую он затем продаст на рынке. Г-н "А" продал заимствованную акцию и таким образом получил $100 от покупателя. Ситуация такова:
- Г-н "А": Г-н "А" отдал в залог $100 г-ну "ХМ", получив $100 от покупателя акции. Таким образом, денежные отношения между ними нейтральны. У г-на "А", однако, существует обязательство перед г-ном "ХМ" вернуть акцию в течение некоторого времени в будущем. Так как у г-на "А" такой акции нет, то он, по сути, продал ее без покрытия. В какой-то момент времени в будущем он должен будет достать (т.е. купить) акцию на рынке для того, чтобы вернуть ее г-ну "ХМ".
- Г-н "ХМ": Г-н "ХМ" владеет залогом в $100 и зарабатывает на проценте от депозита. Он находится все еще в длинной позиции, потому что в действительности он ничего не продал, а только одолжил несколько акций г-ну "А". Поэтому г-н "ХМ" все еще находится в длинной позиции (по договору с г-ном "А") и имеет при этом преимущество, которое заключается в том, что он получает дополнительный доход на свои фонды.
На практике зарабатываемый процент от депозита разделяется между г-ном "ХМ" и г-ном "А" согласно договору, называемому договором "репо1" (repo agreement). Мы продолжим этот пример и посмотрим, что произойдет по двум сценариям, которые возможны в действительности.
- Сценарий 1. Цена акции упала до $80. Поэтому г-н "А" входит в рынок, покупает акцию по $80 и отдает ее г-ну "ХМ". Г-н "ХМ" отдает залог в $100, и на этом сделка завершена. Г-н "ХМ" все еще находится в длинной позиции и радуется дополнительному доходу (или доле от него). Г-н "А" купил акцию по $80, а продал по $100, получив при этом прибыль в $20.
- Сценарий 2. Цена акции поднялась до $120. Г-н "А" входит в рынок, покупает акцию по $120 и отдает ее г-ну "ХМ". Г-н "ХМ" все еще в длинной позиции и радуется дополнительному доходу (или доле от него). Г-н "А" купил акцию по $120, а продал ее по $100, оказавшись в убытке, составившем $20.
Все это кажется довольно сложным, но для большинства развитых фондовых рынков (за исключением Великобритании) процесс заимствования акций — чрезвычайно эффективный бизнес. Многие участники рынка — крупные, средние или даже совсем небольшие — считают, что идти в короткую так же просто, как идти в длинную.
2.3 Прибыль, убыток и ценовые изменения
Каждый понимает, что это такое — находиться в прибыли или в убытке. Зачастую прибыль и убыток рассматриваются с точки зрения процентных изменений. В мире инвестиций в производные ценные бумаги это приводит к большой неразберихе. Более качественным подходом будет рассмотрение понятий прибыли и убытка с точки зрения абсолютного изменения величины инвестиции, нежели с точки зрения процентного изменения. Также гораздо легче представить прибыль или убыток графическим способом, если использовать абсолютную меру. Соответственно, на протяжении всей книги прибыль и убыток будут описываться с точки зрения абсолютных, а не процентных изменений.
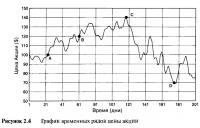
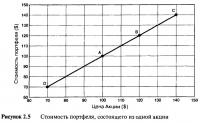
Инвесторы используют при исследовании ценовых графиков акций определенные временные периоды, как например, это дано на Рисунке 2.4, где за основу взят дневной масштаб. Эти графики называют графиками ценовых рядов. На таких диаграммах горизонтальная ось всегда является временем, а вертикальная всегда показывает цену. При покупке в точке "А" и продаже в точке "В", или при продаже без покрытия на "С" и обратной покупке в момент "D" возникает прибыль. Для того, чтобы понять смысл сделок по волатильности, необходимо обратить внимание на различное изображение прибыли и убытка, как это показано на Рисунках 2.5—2.7.
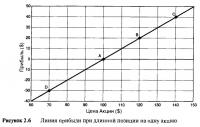
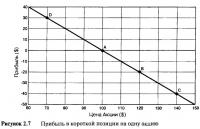
Рисунок 2.5 отражает стоимость портфеля, состоящего из одной акции, в сравнении с ценой акции, что конечно же, предельно просто для понимания. Рисунок 2.6 иллюстрирует изменение стоимости портфеля из одной акции, предполагая, что акция была куплена в точке "А", то есть по цене $100. Этот график показывает прибыль или убыток (в абсолютном смысле) при длинной позиции, состоящей из одной акции. На обоих графиках горизонтальная ось является ценой акции, а не временем. В результате временная последовательность, связывающая точки "А", "В", "С" и "D", потеряна. Также обратите внимание на то, что наклон линий составляет 1 или 100%. Может показаться, что эти выводы и без того очевидны. Но понадобится время, чтобы осознать всю важность этого, на первый взгляд простого способа определения прибыли и убытка через углы наклона прямых линий. Рисунок 2.7 иллюстрирует прибыль и убыток при нахождении в короткой позиции на одну акцию, наглядно представляя наклон —1, или —100%.
2.4 Значение использования экспозиции, а не стоимости при измерении риска
Графики прибылей и убытков на Рисунках 2.6 и 2.7 дают представление еще и об экспозиции по акции (stock exposure). Наклон линии прибылей определяет экспозицию по акции. На Рисунке 2.6 наклон показывает, что инвестор обладает одной акцией. Линия прибыли полностью прямая, поэтому наклон при всех ценовых уровнях акции постоянно один и тот же. Когда у вас длинная позиция из одной акции, то ваша экспозиция по акции всегда составляет одну акцию, какова бы ни была ее цена. На Рисунке 2.7 наклон постоянно "—1" при всех ценовых уровнях. Когда у вас короткая позиция из одной акции, то экспозиция вашей акции всегда обратная той, которая была бы при вашем нахождении в длинной позиции, какова бы ни была цена акции.
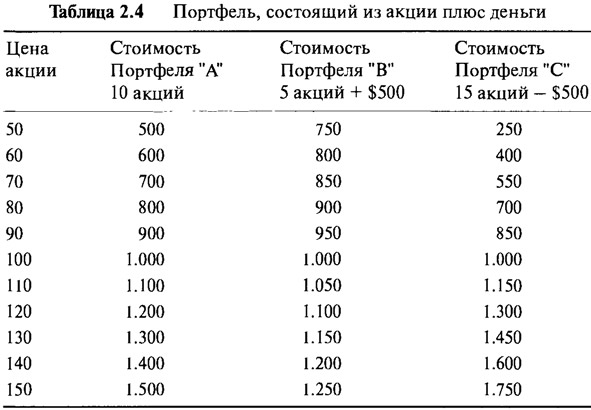
Таблица 2.4 показывает стоимость трех портфелей "А", "В" и "С" в диапазоне различных цен акций. Трем руководителям фондов дали по $ 1.000 и сказали, что они могут инвестировать только в определенную акцию (сегодняшняя цена которой $100) и/или сохранять деньги в виде наличности. Они вправе оставить часть или все деньги на депозите, либо занять максимум $500 для дальнейшего инвестирования. Для упрощения предположим, что они не получали никаких процентов по депозиту, а стоимость заимствования равна нулю. Управляющий портфелем "А" покупает 10 акций по $100, тратя полностью выделенную ему сумму: 10x100=$ 1.000, таким образом инвестируя 100% в акцию. Управляющий портфелем "В" решает быть более осторожным и покупает 5 акций, тратя 5х100=$500 и оставляя $500 на депозите. Управляющий портфелем "С", уверенный в отношении перспектив ценового развития акции, занимает $500, что вместе с первоначальными $ 1.000 позволяет ему купить 15 акций.
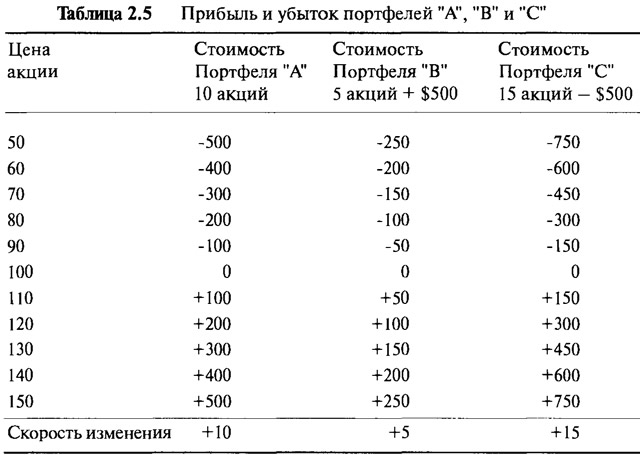
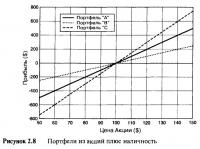
Таблица 2.5 и Рисунок 2.8 показывают прибыли и убытки портфелей. Цифры получены путем вычитания первоначальной стоимости инвестиции в $1.000 из стоимостей соответствующих портфелей, указанных в Таблице 2.4. Наклоны линии прибылей "А", "В" и "С" равны 10, 5 и 15 соответственно. Эти наклоны точно отражают подверженность риску, связанному с акциями. Рыночная цена (или стоимость) портфелей не учитывается. Если три фонда оценивались бы в момент их создания, то они имели бы одну и ту же стоимость в $1.000. Распространенная ошибка, в особенности на рынке производных финансовых инструментов, заключается в том, что при покупке чего-либо за $1.000, многие полагают, что это и есть весь риск, которому подвержен покупатель. Определенно, это совсем не так. Инвесторы, покупающие фонды "А", "В" и "С", подвергаются совершенно различным рискам. Цена здесь ни при чем. Важна скорость изменения цены. Необходимо уметь оценить, насколько динамично будет развиваться инвестиция по мере движения цены базовой акции. И здесь нужно уметь вычислять скорость изменения или наклон профиля прибыли.
2.5 Нелинейный профиль прибыли воображаемого инвестирования
Углы наклона профилей прибыли и убытка вышеприведенных портфелей "А", "В" и "С" остаются постоянными на всем протяжении ценового диапазона акций. Таким образом, экспозиция акции каждого портфеля оставалась фиксированной на любом ценовом уровне. Это необычно для портфелей, содержащих производные финансовые инструменты. На самом деле, все примеры были подобраны специально для того, чтобы показать, что этого не происходит при торговле волатильностью. Прежде чем мы отправимся дальше, будет полезно посмотреть, какие изменения в части прибылей и убытков коснутся того, кто инвестировал в инструмент, имеющий различные экспозиции по акции.
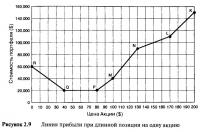
В качестве примера возьмем воображаемый портфель "черный ящик". Содержимое портфеля "черный ящик" неизвестно. Все, что сказано о нем, — это то, что стоимость портфеля меняется по мере изменения цены определенной акции. Взаимосвязь между стоимостью портфеля и ценой акции показана в Таблице 2.6 и на Рисунке 2.9.
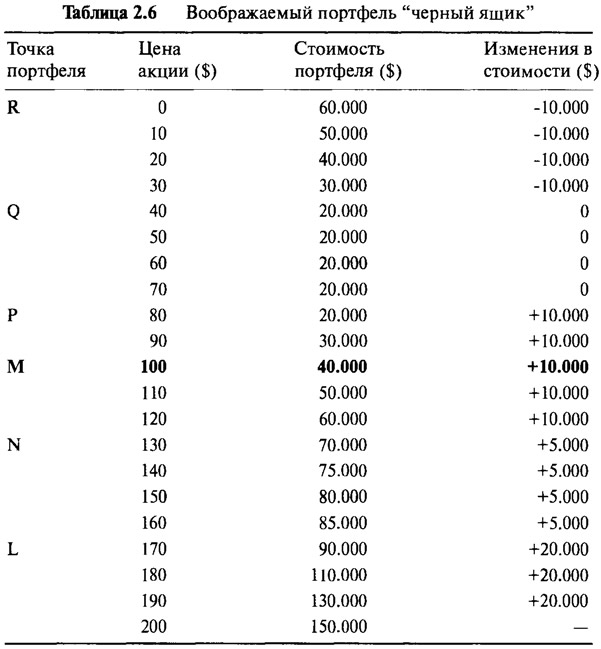
- Зона от "Р" до "N". Рассмотрим ситуацию того дня, когда цена акции равна $100, а стоимость портфеля оценивается в $40.000. Мы покупаем акцию, включая ее в портфель, или открываем длинную позицию на $40.000. Наше местоположение — точка отмеченная на Рисунке 2.9 как "М". Сразу же после покупки цена акции начала изменяться. Сначала вверх на $10, достигнув $110, а потом вниз на $20 — до $90. Обратите внимание, что стоимость портфеля "черный ящик" также меняется. При повышении цены акции на $10 стоимость портфеля увеличивается на $10.000. При падении цены акции на $20 стоимость портфеля падает на $20.000. Создается "ощущение", что портфель состоит из длинной позиции на 1.000 акций, то есть экспозиция акции составляет 1.000 акций. Обратите внимание, что портфель на самом деле стоит только $40.000. Для того чтобы добиться такой же экспозиции акции, нужно заплатить 1.000x100=$ 100.000. Хотя мы инвестировали только $40.000, ситуация возле точки "М" такова, будто мы инвестировали в акции, чья стоимость составляет $100.000. Это вполне реально. Просто вспомните простой прием, описанный в разделе 2.4, с помощью которого менеджер фонда занял средства, чтобы повысить экспозицию.
- Зона от "N" до "L". Давайте представим, что цена акции поднялась выше $130, то есть выше точки "N". Между "N" и "L" угол наклона профиля стоимости сокращается наполовину, до 500. Нам неизвестно, что происходит внутри портфеля, мы знаем только то, что последующее повышение цены акции на $10 приводит к дополнительной прибыли в $5.000. Внезапно мы оказываемся в ситуации, в которой экспозиция составляет только половину от количества акций, в сравнении с предыдущим, только что описанным случаем. Это как если бы руководитель фонда "черный ящик" продал половину акций в точке "N". Между "N" и "L" экспозиция по акции равна 500 единицам.
- Зона от "L" до "К". Если цена акции продолжает расти выше точки "L", то мы оказываемся в другой ситуации. Теперь при каждом повышении на $10 стоимость портфеля увеличивается на $20.000. Наклон линии, а следовательно экспозиция по акции теперь составляет 2.000.
- Зона от "Р" до "Q". Рассмотрим ситуацию, при которой цена акции все время падает, находясь ниже отметки в $80, но выше $40, то есть между "Р" и "Q". Между этими двумя точками стоимость портфеля постоянно равна $20.000 и совсем не зависит от цены акции. Наклон линии и, следовательно, экспозиция по акции равны нулю. Это как если бы руководитель фонда полностью продал все содержимое, оставив только деньги в сумме $20.000.
- Зона от "Q" до "R". Ниже $40 (точка "Q") мы имеем обратную ситуацию, а именно: по мере того, как цена падает на $10, стоимость портфеля увеличивается на $10.000. Наклон линии "QR" — 1.000. Явно, что экспозиция по акции здесь имеет отрицательное значение, или — короткая позиция на 10.000 акций.
Цель этого наглядного примера состоит в том, чтобы подчеркнуть, что экспозиция инвестирования в акции может и не иметь ничего общего со стоимостью инвестиции и что экспозиция бывает постоянной, а также линейной. Все дело в чувствительности инвестиции к движению цены акции. Чувствительность, или экспозиция, акции измеряется углом наклона графика цены инструмента, являющегося предметом инвестиции, а не действительным уровнем, или стоимостью инвестиции. При торговле волатильностью мы намеренно создаем портфели таким образом, чтобы экспозиция постоянно менялась наряду с ценой базовой акции.
2.6 Реальный пример нелинейного ценового профиля
Портфель "черный ящик", о котором шла речь в разделе 2.5, — это искусственный инструмент, который был использован только в качестве примера. Однако существуют реальные инструменты, проявляющие некоторые нелинейные свойства приблизительно такого же рода. Одним из таких примеров является конвертируемая облигация (СВ — Convertible Bond). "СВ" выпускаются корпорациями для привлечения капитала в свой собственный бизнес. Самая простая "СВ" предполагает выплату фиксированного процентного дохода по облигации, рассчитанную на годовой основе, и может быть погашена как обычная облигация или конвертирована (converted) в акции. Владелец "СВ" тем самым становится перед выбором: либо погасить облигацию и получить деньги, либо превратить ее в акции. Ни в том, ни в другом случае никаких дополнительных затрат не требуется. У "СВ" есть фиксированная дата погашения, поэтому ее владельцу, в конце концов, придется выбрать что-то одно: деньги или акции. Рассмотрим следующий простой пример.
"СВ", конвертируемая в одну акцию, в скором времени должна быть погашена. Выкупная стоимость "СВ" равна $100, и нет каких-либо других причитающихся к выплатам процентов.
- Цена акции $110. Сколько будет стоить "СВ", если в день погашения цена акции будет равна $110? Очевидно, что владелец решит взять акции и немедленно продать их на рынке, получив за них взаимен $110 за каждую. Нет никакого смысла погашать облигацию за фиксированную сумму в $100.
- Цена акции $120. Сколько будет стоить "СВ", если в день погашения цена акции будет равна $ 120? Очевидно, что владелец решит взять акции и немедленно продать их на рынке, чтобы получить $120. На самом деле, при любой цене выше $100 всегда разумней превратить облигацию в акции.
- Цена акции будет равна $90? В этом случае конвертировать в акции нет смысла. Будет лучше взять $100. При цене ниже $100 всегда разумнее выбрать деньги.
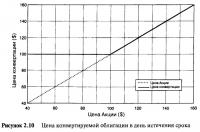
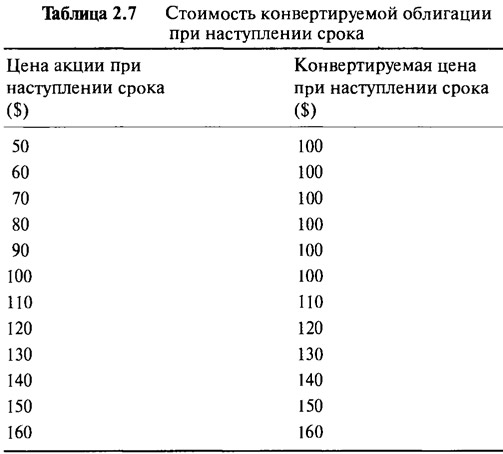
Таблица 2.7 и Рисунок 2.10 показывают стоимость "СВ" в день погашения при различных ценовых уровнях акции. Профиль цены явно нелинейного характера. При цене акции свыше $100 наклон линии проявляет себя единообразно: инструмент ведет себя точно так же, как простая акция. При стоимости акции ниже $100 наклон равен нулю: инструмент совершенно независим и ведет себя подобно денежному пулу в $100. Такова ситуация со всеми "СВ" в день погашения. Нелинейность, а точнее, перелом на $100, объясняется тем, что у владельца есть выбор (option) предпринять то или другое действие. Именно факт того, что владелец может выбирать при наступлении срока (on maturity) между акциями или деньгами, влияет на оценивание инструмента до наступления срока (before maturity). Именно оценивание такого инструмента до наступления срока погашения считается более сложным, и аспекты этого мы рассмотрим подробнее в Главе 3.
2.7 Измеряя волатильность
Каждый, кто связан с финансами или инвестициями, встречается с понятием волатильности. Во время всем известного краха фондовой биржи в октябре 1987 года Индекс Доу-Джонса, включающий в себя акции промышленных компаний, за один день упал на 512 пунктов (25%) и на следующий день повысился всего на 60 пунктов. Это привело к крахам на других биржах и, как следствие, к росту волатильности цен на биржевых рынках по всему миру. Хотя и считается, что наибольший рост рыночной волатильности связан с большими падениями цен, истинная причина не всегда кроется именно в этом. В 1979 году цена на золото увеличилась на 200% всего за шесть месяцев, а в 1990 году стоимость сырой нефти за три месяца выросла на 160% , что привело к Войне в Персидском Заливе2.
Фондовые рынки, охваченные паникой инвесторов, переводящих активы в деньги или товары, зачастую устанавливают свои правила игры, заставляя инвесторов менять тактику, и тогда продавцы ценных бумаг, игравшие на понижение, начинают покупать акции по более высокому курсу, опасаясь еще большего роста цен. Кризис механизма контроля курса валют Европейского экономического сообщества (ERM) в Британии в 1992 году стал причиной того, что краткосрочная рыночная процентная ставка неестественно увеличила волатильность. Ставки по фунту двигались от 10 к 12 и даже к 15%, а потом назад к 10% — и все это в течение одного дня.
Хотя многие имеют представление о том, что такое волатильность, мало кто знает, как она измеряется, а многие просто путают ее с направлением. Эта книга объясняет, что означает покупать или продавать волатильность, поэтому очень важно понять, как измеряется волатильность. При открытии длинной или короткой позиции по волатильности важно иметь представление о том, какая волатильность ожидается в будущем и что это в действительности означает с точки зрения ценовых изменений.
Точное определение волатильности, которым пользуются участники рынка, довольно сложное и подразумевает использование натуральных логарифмов и знание статистики, связанной с таким понятием, как логнормальное (или логарифмически нормальное) распределение (lognormal distribution). Однако можно объяснить принцип измерения волатильности, пользуясь более простыми понятиями, что мы и собираемся сделать. Несмотря на то, что нижеприведенные примеры довольно просты, следует заметить, что они выбраны нами только для объяснения. Точное же определение волатильности при необходимости можно найти в большинстве учебников по калькуляции цен опционов (премий). Также следует заметить, что в действительности многим участникам рынка не стоит утомлять себя вычислениями волатильности ценовых рядов. Большинство служб информации, таких как Bloomberg и Reuters, предоставляют расчеты исторической волатильности, а многие аналитические пакеты еще и позволяют создавать прекрасные графики, отражающие то, как волатильность данных рядов изменялась на протяжении каких-либо периодов времени. В дополнение к расчетам исторической волатильности, эти службы также публикуют информацию о так называемой подразумеваемой волатильности (implied volatility). Подразумеваемая волатильность является, несомненно, одним из наиболее важных измерений для игрока волатильностью, и она будет рассмотрена ниже.
Термин "волатильность ценового ряда" на самом деле употребляется неправильно. Когда профессионалы говорят о волатильности ценового ряда, они имеют в виду волатильность рядов ценовых изменений (price changes), или относительных ценовых изменений. Что касается понятия экспозиции по акции, то необходимо осознавать, что цена исследуемой акции не имеет никакого значения. Изменение цены — вот что важно. В отношении многих понятий в инвестиционной отрасли имеет значение не ценовой уровень, а то, как изменяется цена. Мы можем думать об изменениях ценовых рядов, как о "вызванных" течением времени. При измерении волатильности нам интересно то, как временной поток воздействует на изменения цены.
Сложность, связанная с обзором ценовых рядов и ценовых изменений, объясняется наличием тенденции. Волатильность предназначена измерять степень колебаний, а не тенденции. Если существует тенденция, тогда мы должны рассматривать колебания вокруг этой тенденции. Если цена акции выше (ниже) в конце периода, чем в начале, то мы говорим, что наблюдается положительная (отрицательная) тенденция. Это утверждение подкреплено специально составленными диаграммами на Рисунке 2.11. Числа подобраны таким образом, чтобы ряды имели идентичную тенденцию. Ценовой ряд (I) начинается в первый день на $100 и равномерно увеличивается на $1 в день на протяжении десяти дней. Ценовой ряд (II) также начинается в первый день на $100, но увеличивается неравномерным образом. Оба ряда заканчиваются на той же самой цене, поэтому имеют одинаковую тенденцию: в среднем +$ 1 в день. Вторая диаграмма на Рисунке 2.11 показывает соответствующие ежедневные изменения цены. Понятно, что ряды (II) демонстрируют волатильность, а ряды (I) — нет. Все изменения в рядах (I) равны $1, в то время как в рядах (II) они различны. Среднее значение изменений, или тенденция, обоих рядов составляет $1 в день, но что касается рядов (II), то здесь существуют некоторые отклонения от среднего показателя. И это подводит нас к определению волатильности.
Волатильность ценового ряда является мерой (степенью) отклонения ценовых изменений относительно тенденции.
Хотя это определение и кажется сложным, найти ее значение довольно легко. Детали расчета для рядов (II) приведены в Таблице 2.8.
Колонка (с) в Таблице 2.8 отражает отклонения изменений относительно среднего значения тенденции. Мера волатильности, которую мы ищем, является одной цифрой, суммирующей значения всех этих отклонений. Если эти отклонения большие, то мы говорим, что ряды очень волатильны, а если они маленькие, мы говорим, что ряды не очень волатильны. Нам нужен только один количественный показатель распределения, который выясняется сложением всех средних значений отклонений и, вполне очевидно, что он станет средним показателем. Однако по определению некоторые из этих отклонений положительны, а другие — отрицательны, и легко доказать, что они всегда будут уравновешивать друг друга, и что окончательное значение, а следовательно, и среднее значение всегда будут равны нулю. Это означает, что нельзя использовать средний показатель. Мы легко найдем решение, если будем учитывать, что нас интересуют только величина отклонений, а не их знаки. Нам известно, что все положительные отклонения всегда равны негативным отклонениям, поэтому мы будем рассматривать только абсолютные значения, колонка (d). Среднее значение этой колонки "-1,8", и мы считаем его средним отклонением от значения тенденции. Это и есть волатильность рядов. Ряды II являются последовательностями цен, которые имеют среднюю тенденцию $1 в день с волатильностью вокруг этой тенденции $1,8 в день. Теперь читателю самому осталось доказать, что ряды I имеют нулевую волатильность.

Рисунок 2.12 показывает три смоделированных ценовых ряда с различными степенями волатильности и тенденции. В этих рядах значение волатильности выражено в количестве "N" долларов в неделю. Наиболее волатильные ряды имеют среднюю величину отклонения (волатильности) $4 в неделю. Можно выразить эту волатильность в процентах от исходной цены акции и сказать, что волатильность составляет 4% на недельной основе. Таким образом, мы можем сравнить две акции: одну, торгуемую по $100 и другую, торгуемую по $200. Если обе имеют одну и ту же волатильность в процентном выражении, тогда вторая акция будет располагать средним колебанием в $8 вокруг среднего значения тенденции.
Точное определение волатильности, которым пользуются участники рынка, подразумевает волатильность как функцию относительных ценовых изменений, а не самих ценовых изменений. Результаты измерения волатильности всегда даются в годовых процентах, даже если рассматриваемый период времени составляет только три месяца. Обычные значения волатильности могут составлять 20% для отдельной акции, 13% для фондового индекса и 40% для высоковолатильного товара. Точное толкование абсолютного измерения отклонения волатильности, которым мы пользовались в вышеприведенных примерах, достаточно простое. Что же касается стандартного, которым пользуются участники рынка, то оно более сложное. Однако оба они измеряют одно и то же значение: степень ценового отклонения от некоторой средней величины тенденции. Использование стандартного способа измерения волатильности необходимо для определения приблизительного диапазона цены акции в будущем. Предполагая, что стандартная волатильность рядов составляет х %, тогда за период, равный одному году:
- 1. Существует 66% вероятности, что цена акции будет находиться в диапазоне от (100 — х) % до (100 + х)% от сегодняшней цены.
- 2. Существует 95% вероятности, что цена акции будет находиться в диапазоне от (100 — 2х) % до (100 + 2х)% от сегодняшней цены.
- 3. Существует 99% вероятности, что цена акции будет находиться в диапазоне от (100 — Зх) % до (100 + Зх)% от сегодняшней цены.
Итак, если цена акции сегодня равна $200, а волатильность акции 25%, тогда существует 66% вероятность того, что цена акции будет находиться в диапазоне от $150 до $250. Эти цифры приблизительны, но они дают представление о вероятном диапазоне будущих цен.
Существует много способов проведения выборки для вычисления волатильности. Используем ли мы дневные, недельные или месячные цены? Какой берем временной интервал? Точность всех используемых статистических данных является необходимым условием выборки. Использовать 200 элементов выборки лучше, чем только 50. Но на сколько недель назад — на 200 или на 50 — мы должны вернуться в прошлое для определения волатильности цены акции IBM? Если отсчитать 200 недель, то мы можем включить данные, которые уже настолько устарели, что скорее увеличат, нежели уменьшат вероятность ошибки. Наш опыт подсказывает, что волатильность постоянно изменяется, поэтому лучше изучать не очень большой временной интервал. Другой способ заключается в использовании внутридневных данных. Выше мы использовали только одну цену за день, и многие участники рынка пользуются данными, полученными на основе дневных цен закрытия. Некоторые же трейдеры используют для своих вычислений большее количество показателей — это цены открытия, максимальные, минимальные и цены закрытия.
К сожалению, невозможно вычислить точное значение волатильности. Как и многое другое в финансовом деле, все вычисления, как бы они не были сделаны, всегда будут временными, поэтому не следует полагать, что волатильность, рассчитанная в прошлом, — это удачный прогноз будущей волатильности. Из этого не следует, что вычисления волатильности на определенный период времени бесполезны. Это означает лишь то, что нужно быть осторожным с полученным результатом. Практика подтверждает то, что называется "возращением к средней величине" волатильности. Проще говоря, если определенный ценовой ряд начинает демонстрировать высокую волатильность, то она, в конце концов, понизится. Точно также, если ряд начинает демонстрировать чрезвычайно низкую волатильность, она в конечном итоге поднимется. Теория предполагает существование некоторого долгосрочного уровня средней волатильности. Ее суть, безусловно, заключается в определении высоких и низких значений волатильности.
Примечания
1. Repo Agreement or Repurchase agreement — Репо Договор - это соглашение о покупке ценных бумаг с последующим выкупом по обусловленной цене.
2. Автор исходит из той идеи, что ситуация на рынках подтолкнула к принятию решения о необходимости разрешения конфликта военным путем. Данное утверждение спорно, но и не беспочвенно. Вместе с тем следует отметить, что сторонники технического анализа выразились бы по-иному: "Рынок предвидел экстремальные события в будущем, поэтому цены резко поднялись".