- 62, 63. Обсуждение, ограниченное случаем, когда кривые предложения непрерывны и имеют один максимум.
- 64. Кривые предложения не пересекаются с кривыми спроса; отсутствие текущей цены.
- 65. Кривые предложения пересекают кривые спроса в трех точках; три текущие цены.
- 66, 67, 68. Две цены устойчивого равновесия; одна цена неустойчивого равновесия.
- 69. Одна из двух кривых спроса совпадает с гиперболой наличного количества.
- 70. Каждая из двух (кривых).
62. Резюмируем. Если даны два товара (А) и (В), для которых отношение между действительным спросом и ценой выражается уравнениями
то равновесная цена дана уравнением
или, заменяя Da и Db на их значения, уравнением
которое можно представить в форме
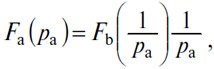
или в форме
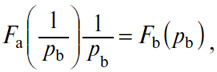
в зависимости от того, хотим мы вывести pa или pb. Первая из этих двух форм выражает, что Da=Oa, вторая — что Ob=Db.
Мы решили уравнение в двух его формах через пересечение кривых
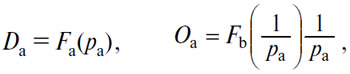
и кривых

но это решение необходимо обсудить.
63. Мы не будем его обсуждать для всех возможных случаев, что было бы слишком долгим и, впрочем, преждевременным делом, а только для достаточно простого общего случая, к которому относится наш рисунок. Мы сделали предположение (рис. 2) о наличии двух непрерывных кривых AdAp, BdBp, имеющих к тому же один максимум для прямоугольников с координатами Dp, Dbpb между точкой, для которой pa=OAp и Da=0, и точкой, для которой pa=OAp и Da=0, между точкой, для которой Db=OBd и pb=0, и точкой, для которой pb=OBp и Db=0. Впрочем, нам следует рассмотреть лишь часть этих кривых, заключенную в плоскости положительных координат, и в ней отрезок, заключенный между точками Ad и Ap, между точками Bd и Bp. Это вытекает, разумеется, из самой природы факта обмена. При данном допущении кривые KLM, NPQ являются непрерывными и имеют лишь один максимум по ординатам. Однако даже в ограниченном случае, определенном подобным образом, есть материал для интересного обсуждения.
64. Мы рассуждали так, как если бы AdAp и KLM, с одной стороны, и BdBp и NPQ, с другой, пересекались в одной точке А и в одной точке В. Но следует прежде всего заметить, что эти кривые могли бы не пересечься вовсе. Если бы, действительно, кривая BdBp приближалась к оси цен в точке, расположенной ближе к центру, чем точка N, то она не пересеклась бы с кривой NPQ. Впрочем, в этом случае и кривая KLM сдвинулась бы по оси цен за точку Ap, и кривая AdAp ее бы не пересекла. В этом случае решения не было бы.
В данной вероятности нет ничего удивительного. Она соответствует случаю, когда ни один держатель блага (В) не хочет отдавать количества Ap этого блага за 1 единицу блага (А), или 1 единицу (В) за 1/Ap единиц блага (A), в то время как, с другой стороны, ни один держатель (А) не хочет отдавать 1/Ap (A) за 1 единицу (В), или 1 (A) за Ap (B). Очевидно, что торг не дал бы в этом случае на рынке никакого результата. Если бы в качестве цены (А) в (В) предлагалась цена ниже Ap, т.е. в качестве цены (В) в (А) предлагалось больше 1/Ap, то был бы спрос на (А) со стороны держателей (В), но не было бы спроса на (В) со стороны предлагающих (А). А если бы предлагалась цена ниже 1/Ap в качестве цены (В) в (А), т.е. выше Ap в качестве цены (А) в (В), то был бы спрос на (В) со стороны предлагающих (А), но не было бы спроса на (А) со стороны предлагающих (В).
65. Внимательное рассмотрение формы кривых позволяет заметить, наряду с предыдущим, и тот случай, когда у кривых может быть несколько точек пересечения. Если бы, действительно, два товара (А) и (В) были таковы, что (имея в виду, что спрос на (А) в (В) также выражается кривой AdAp) спрос на (В) в (А) был бы представлен кривой B'dB'p, то кривая B'dB'p пересекалась бы кривой NPQ в трех точках — В, B', B". В этом случае вместо кривой KLM предложения (А) на (В) была бы кривая K'L'M', которая сама пересекала бы кривую AdAp в трех точках A, A', A", точка А соответствовала бы точке В, точка A' — точке B', точка А' — точке B". Тем самым имелось бы три разных решения задачи обмена двух товаров (А) и (В) друг на друга, поскольку имелось бы три системы, каждая из которых имела бы по два вписанных в кривые AdAp, B'dB'p прямоугольника, длины оснований которых являются обратными величинами, а отношения высот которых обратно пропорциональны отношению их площадей. Однако равнозначны ли эти три решения?
66. Если из трех систем мы рассмотрим сначала те, которые относятся к точкам A' и B', A" и B', то окажемся в условиях, тождественных условиям системы, относящейся к точкам А и В в случае одного единственного решения. Справа или слева от точки А', где пересекаются обе кривые AdAp и K'L'M', кривая AdAp лежит ниже или выше кривой K'L'M'; и, равным образом, справа или слева от точки B', где пересекаются кривые B'dB'p и NPQ, кривая BdBp ниже или выше кривой NPQ. Справа или слева от точки А' кривая AdAp лежит ниже или выше кривой K'L'M'; и, равным образом, справа или слева от точки B" кривая B'dB'p ниже или выше кривой NPQ.
В обоих случаях, когда точки лежат дальше от начала координат, чем точка равновесия, предложение товара больше спроса на него, что должно привести к понижению цены, т.е. к возврату к точке равновесия. В обоих случаях, когда они лежат ближе точки равновесия, спрос на товар больше его предложения, что должно привести к повышению цены, т.е. к движению в сторону точки равновесия. Можно, следовательно, сравнить это равновесие с равновесием висящего тела, точка опоры которого находится выше центра тяжести по вертикали, так что в случае отклонения этого центра тяжести от вертикали он вернется сам по себе в прежнее положение под действием одной силы тяжести. Это — устойчивое равновесие.
67. Иначе обстоит дело с точками А и В. Справа от точки А кривая AdAp находится выше кривой K'L'M', слева от нее она ниже. Равным образом, справа от точки В кривая B'dB'p лежит выше кривой NPQ, слева от нее — ниже. Таким образом, в этом случае, если мы находимся дальше точки равновесия от начала координат, спрос на товар больше его предложения, что должно привести к повышению цены, т.е. к удалению от точки равновесия. И также в этом случае, когда мы находимся от точки равновесия ближе к началу координат, предложение товара больше спроса на него, что должно привести к понижению цены, т.е. также к удалению от точки равновесия. Данное равновесие в точности сравнимо с равновесием тела, точка опоры которого находится ниже центра тяжести по вертикали, так что если центр тяжести ушел от вертикали, то он все более и более отклоняется от нее и под действием одной лишь силы тяжести может вернуться к вертикали лишь ниже точки опоры. Это — неустойчивое равновесие.
68. В действительности системы (пары точек) A' и B', а также A" и B" представляют, следовательно, два единственных решения задачи, а система А и В представляет собой лишь точку разделения и границу соответствующего поля каждого из этих двух решений. При значениях, превышающих pb=μ, цена (А) в (В) стремится к равновесной ценеp'b, абсциссе точки В"; при меньших значениях она стремится к цене pb, абсциссе точки B. Соответственно при значениях, меньших pa=1/μ, цена (А) в (В) стремится к равновесной цене p"a, абсциссе точки A"; при больших значениях она стремится к цене p'a, абсциссе точки A'.
Эта вероятность соответствует, как нетрудно видеть, случаю, когда в силу природы товаров оказывается, что большое количество товара (А), запрашиваемое по низкой цене, может быть равноценным малому количеству товара (В), запрашиваемому по высокой цене (В) в (А), в то же время малое количество (А), запрашиваемое по высокой цене (А) в (В), может также быть равноценным большому количеству (В), запрашиваемому по низкой цене (В) в (А). В этом случае в зависимости от того, начнутся ли торги с низкой цены (А) в (В) и высокой (В) в (А), или же с низкой цены (В) в (А) и высокой (А) в (В), то они приведут к первому или второму из указанных равновесий. Ниже мы увидим, остается ли возможным данный вариант при нескольких товарах, обменивающихся друг на друга с участием счетного товара и денег.
69. До сих пор в ходе нашего обсуждения мы предполагали, что кривые спроса AdAp, BdBp, B’dB’p пересекают обе оси координат. Надо рассмотреть крайний случай, когда кривые спроса, совпадая с гиперболами наличного количества, оказываются асимптотами к этим осям.
Если, например, AdAp сливалась бы с гиперболой Dapa=Qb, а товар (В) предлагался бы по любой цене, то уравнение [1] стало бы следующим:
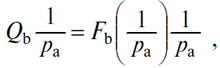
которое представляло бы пересечение в pa кривой, проходящей через точку Qb, и кривой KLM. Я абстрагируюсь от решения, даваемого уравнением 1/pa=0, т.е. pa=∞.
Уравнение [2] стало бы в данном случае
которое представляет пересечение в pb кривой BdBp и прямой N'P'Q', проведенной параллельно оси цен на расстоянии ON'=Qb.
70. Наконец, если бы оба товара предлагались по любой цене, то мы имели бы одновременно

что дало бы при соответствующих значениях pa и pb

Таким образом, в этом последнем случае оба товара обменивались бы просто-напросто в обратной пропорции наличного количества, т.е. согласно уравнению,
И, действительно, как нетрудно признать, это равенство наличных количеств и обмененных количеств представляло бы собой в таком случае само равенство действительных объемов предложения и спроса по обоим товарам.
