Формула математического решения задачи обмена двух товаров

Содержание:

• 85. Спрос при нулевой цене; он равен экстенсивной полезности.
• 86. Цена, при которой спрос на (А) равен нулю.
• 87, 88. Цена, при которой предложение (В) равно имеющемуся количеству: пересечение гиперболы имеющегося количества и кривой спроса.
• 89. Гипербола — кривая спроса между точками пересечения.
• 90. Уменьшение имеющегося количества.
• 91. Увеличение.
• 92. Общий случай — случай одного держателя обоих товаров. Два уравнения или кривые частичного действительного спроса.
• 93, 94, 95. Уравнение или кривая спроса на каждый товар — это также уравнение или кривая спроса на тот же товар в зависимости от цены.
• 96. Общая система уравнений намерений к торгу в случае обмена двух товаров друг на друга.
• 97, 98. Решение уравнений.

85. Поскольку уравнение частичного спроса


является не чем иным, как уравнением


которое предполагается решенным относительно d_a, мы можем обсудить его в этом последнем виде.

Сделаем сначала p_a=0, тогда уравнение сводится к


корень которого — d_a=α_q,1=Oa_d,1.


Итак: если на рынке даны два товара, то, когда цена одного из них равна нулю, количество этого товара, запрашиваемое каждым держателем другого, равно количеству, необходимому для удовлетворения всех потребностей вдоволь, или экстенсивной полезности.

Так и должно, действительно, быть. Кривая a_d,1a_p,1 начинается из точки a_q,1.

86. Положим теперь в уравнении спроса d_a=0, получим


уравнение, корень которого есть


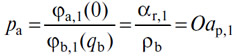
Итак: количество одного из двух товаров, запрашиваемое держателем другого (товара), равно нулю, если только цена этого товара равна или больше отношения интенсивности максимальной потребности в нем к интенсивности последней потребности, которая может быть удовлетворена имеющимся количеством товара, предлагаемого в обмен.

Действительно, именно это должно иметь место, так как в этом случае последний элемент (В), например o_b/s, потребляемый держателем (1), приносит ему удовлетворение (o_b/s)p_b, а тот же самый элемент, обмененный на d_a/s (A) по цене p_a, принесет ему удовлетворение всего лишь (d_a/s)a_r,1 = o_ba_r,1/sp_a, равное или меньшее, чем первое.

87. Выявив ценовое условие, необходимое для того, чтобы наш держатель (1) товара (В) не предъявлял спроса на (А), попробуем выявить условие, необходимое для того, чтобы он не удерживал (В) для себя. В уравнении



надо сделать


Тогда оно становится


уравнением, чей корень есть


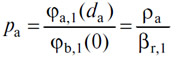
Итак: количество одного из двух товаров, предлагаемое держателем этого товара, равно имеющемуся количеству, когда цена запрашиваемого товара равна или меньше отношения интенсивности последней потребности, которая может быть удовлетворена этим товаром, к интенсивности максимальной потребности в предлагаемом товаре.


Именно это также должно иметь место, так как в этом случае первый элемент (В), например o_b/s, потребляемый держателем (1), принесет ему всего лишь удовлетворение o_b/sβ_r,1, а тот же самый элемент, обмененный на d_a/s (A) по цене p_a, принесет ему удовлетворение d_ap_a/s=o_bp_a/sp_a, равное или большее, чем первое.

88. Умножив соответственно левые и правые части двух уравнений [2] и [3] и разделив каждую часть на p_a с тем, чтобы исключить это последнее количество, получим


или же, заменяя q_b и φ_b,1(0)=β_r,1 на длины Oq_b, Oβ_p,1, которые их представляют


Это уравнение выражает следующее условие: чтобы предложение одного из двух товаров могло быть равно имеющемуся количеству данного товара, необходимо, чтобы в кривую потребности в запрашиваемом товаре можно было вписать прямоугольник, равный по площади прямоугольнику, высота которого равна имеющемуся количеству предлагаемого товара, а основание — интенсивности максимальной потребности в этом товаре.

Но это условие выполняется не всегда; так, оно не выполняется в нашем примере. Впрочем, его можно заменить другим. Совокупность двух уравнений [1] и [2] представляет собой, в конечном счете, пересечение гиперболы имеющегося количества (В), d_ap_a=q_b, с кривой частичного спроса на (А), d_a=ƒ_a,1 (p_a). Эти две кривые пересекаются не всегда: в частности, они не пересекаются в случае с нашим держателем.


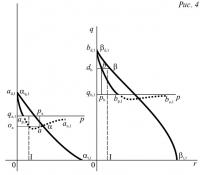
89. Данное замечание влечет за собой другое, крайне важное. Предположим, что удовлетворяется сформулированное выше условие и что кривая спроса пересекается с гиперболой имеющегося количества в точках q'_b и q"_b (Рис. 1). Предложение (В) было бы равно имеющемуся количеству qb при ценах, представленных абсциссами точек q'_b и q"_b. Это равенство имело бы также место при промежуточных ценах. Даже, исходя из комбинации уравнений или кривых, представляется, что при промежуточных ценах предложение (В) должно было бы быть больше имеющегося количества q_b. Но поскольку держатель не может предложить больше, чем имеет, надо, естественно, ввести такое ограничение, что q_b — d_ap_a не может быть отрицательным количеством, а это можно сделать, сформулировав условие в следующих терминах: — Чтобы предложение одного из двух товаров могло быть равным имеющемуся количеству, необходимо, чтобы гипербола данного имеющегося количества данного товара пересекалась с кривой спроса на другой товар. Гипербола количества есть кривая спроса между двумя точками пересечения.

90. Если кривые α_r,1α_q,1, β_г,1β_q,1 (рис. 3) не изменяются, а q_b начинает уменьшаться, то p_b возрастает и, следовательно, α_r,1/p_b=Oa_p,1 уменьшается. Когда q_b=0, r_b=β_r,1, то отношение α_r,1/p_b совпадает с α_r,1/β_r,1=Oπ. В этом случае кривая спроса a_d,1α_p,1 совпадает с частью осей координат a_d,1Oπ.

Итак: если полезность двух товаров не меняется для держателя одного из них, если имеющееся количество этого товара начинает уменьшаться, то точка пересечения кривой спроса на первый товар с осью цен приближается к началу координат. Когда это имеющееся количество равно нулю, кривая спроса сливается с частью осей координат, образованной — по оси спроса — экстенсивной полезностью запрашиваемого товара, а по оси цен — отрезком, равным отношению интенсивностей максимальных потребностей в обоих товарах.

91. Напротив, если q_b начинает возрастать, то p_b уменьшается и, следовательно, α_r,1/p_b=Oa_p,1 возрастает. Когда q_b=β_q,1, p_b=0, отношение α_r,1/p_b становится бесконечным. Тогда точка a_p,1 бесконечно удалена от точки 0.

Таким образом: если полезность обоих товаров не изменяется для держателя одного из них и если имеющееся количество этого последнего товара начинает возрастать, то точка пересечения кривой спроса на первый товар с осью цен удаляется от начала координат. С того момента, когда это имеющееся количество равно экстенсивной полезности, кривая спроса асимптотически приближается к оси цен.

Мы прекрасно понимаем, что так и должно быть. Впрочем, ясно, насколько мы были правы, отказавшись судить раньше времени о форме кривых совокупного спроса. Сейчас мы могли бы утверждать, что они всегда пересекают ось спроса, так как ни один товар не имеет бесконечной совокупной экстенсивной полезности. Но что касается асимптотического стремления кривой спроса к оси цен, то его следует рассматривать как обычный и частый факт, поскольку он имеет место, если только среди держателей одного из товаров есть один, обладающий этим товаром в количестве, достаточном для полного удовлетворения всех его потребностей. Отсюда следует, что кривые полного предложения начинаются часто от начала координат^*.

92. До сих пор мы постоянно предполагали, что все наши обменивающиеся лица были держателями только одного товара: товара (А) или товара (В). Надо, однако, учесть тот особый случай, когда один и тот же индивид является держателем обоих товаров (А) и (В), и выразить математически его намерения к торгу. Это надо сделать с тем большим основанием, что, в конечном счете, именно этот второй случай является общим, от которого мы приходим к первому, предполагая равным нулю одно из двух наличных количеств. Мы не стали это вводить в задачу обмена двух товаров друг на друга с самого начала из-за возможного усложнения наших рассуждений. Но теорема максимального удовлетворения позволяет теперь рассмотреть его простым и легким образом.

Итак, предположим, что держатель (1) товара (В), потребности которого в (А) и (В) все также выражаются двумя уравнениями r=φ_a,1(q), r=φ_b,1(q) кривых потребностей α_r,1α_q,1,β_r,1β_q,1, вместо того, чтобы прийти на рынок с нулевым количеством (А) и с количеством q_b (B), представленным Oq_b (рис. 3), является на него с количеством q_a,1 (A), представленном Oq_a,1 (рис. 4) и количеством q_b,1 (В), представленным Oq_b,1; а теперь попробуем выразить его спрос на (В) в зависимости от цены p_b и его спрос на (А) в зависимости от цены p_a.

Если при цене p_b товара (В) в (А), представленной длиной q_b,1p_b, он спрашивает количество d_b (В), представленное длиной q_b,1d_b, то он должен будет предложить количество o_a (A), представленное длиной q_a,1o_a, причем такое, чтобы величины p_b, d_b и o_a были связаны уравнением


Так как интенсивность его последней удовлетворенной потребности в (В) есть r_b, представленная длиной d_bβ, а интенсивность его последней удовлетворенной потребности в (А) есть r_a, представленная длиной o_aα, то по теореме максимального удовлетворения мы получим


или, заменяя r_b и r_a на их значения,


уравнение кривой b_d,1b_p,1 спроса на (В) как функции от цены (В) в товаре (А), построенной в осях q_b,1q, q_b,1p.

Равным образом, если при цене р_а товара (А) в (В) наш человек спрашивает количество d_a (А), то он должен будет предложить количество o_b (B), причем такое, чтобы величины p_a, d_a и o_b были связаны уравнением


Так как интенсивность его последней удовлетворенной потребности в (A) есть r_a, а интенсивность его последней удовлетворенной потребности в (B) есть r_b, то мы получим


или


уравнение кривой a_d,1a_p,1 спроса на (A) как функции от цены (A) в товаре (B), постороенной в осях q_a,1q, q_a,1p.

93. Обсуждение двух уравнений [4] и [5] для разных случаев — спроса по нулевой цене, цены при нулевом спросе, предложения, равного наличному количеству, уменьшения или увеличения наличных количеств — будет совершенно аналогичным приведенному выше. Поэтому я не буду этого делать, за исключением особого пункта, который важно отметить.

Если в уравнении [4] принять d_b=0, то оно становится


Поскольку мы имеем, как и раньше, отношение p_ap_b=1, то данное уравнение может быть выражено в форме


Мы могли бы также получить его, принимая в уравнении [5] d_a=0.

Таким образом: если спрос на один из двух товаров при некоторой цене равен нулю, то спрос на другой товар также равен нулю при соответствующей цене.

94. Но данная теорема соответствует более общей теореме.

Чтобы преобразовать уравнение [4] спроса на (В) как функцию от цены (В) в (А) в уравнение предложения (А) как функцию от цены (А) в (В), достаточно заменить в нем d_b на o_ap_a, а p_b на 1/p_a. Тем самым оно станет


уравнение, являющееся не чем иным, как уравнением [5], в котором d_a заменено на (—o_a). Таким образом, уравнение [5] спроса на (А) есть уравнение предложения (А) при отрицательных значениях d_a. Равным образом можно доказать, что уравнение [4] спроса на (В) есть уравнение предложения (В) при отрицательных значениях d_b. Однако, поскольку цены, по существу, положительны, то когда d_b положительно, то o_a=d_bp_b положительно и, следовательно, d_a=—o_a отрицательно; а когда d_b отрицательно, то oa = d_bp_b отрицательно и, следовательно, d_a=—o_a положительно. Равным образом можно было бы доказать, что когда d_a положительно, то d_b отрицательно, а когда d_a отрицательно, d_b положительно.

Итак: если спрос на один из двух товаров при некоторой цене положителен, то при соответствующей цене спрос на другой товар отрицателен, или его предложение положительно.

Действительно, держатель обоих товаров может предъявлять спрос на один из них лишь при условии, что он предлагает другой (товар), и обратно. Отсюда следует, что если он не спрашивает и не предлагает никакого количества одного из них, то он не предлагает и не запрашивает никакого количества другого (товара). Это, как нетрудно признать, тот случай, когда — при равенстве соотношения редкостей двух товаров точно цене одного из них в другом — имеет место максимум действительной полезности.

95. Кривые являются, таким образом, кривыми спроса от точки a_d,1 до точки a_p,1 и от точки b_d,1 до точки b_p,1, а точки a_p,1, b_p,1 являются взаимосвязанными (обратными). А в части, обозначенной на рисунке пунктиром и лежащей ниже осей q_a,1p, q_b,1p, кривые являются кривыми предложения от точки a_p,1 до точки a_o,1 и от b_p,1 до b_o,1. Взятые в целом относительно оси Or, каждая из них является кривой совокупного количества — сохраненного у себя и полученного — каждого из двух товаров в зависимости от цены. Она имеет минимум, соответствующий максимальному предложению в обмен другого товара.

96. Коротко говоря, если мы просто обозначим через х₁ и y₁ количества, положительные либо отрицательные, товара (А) и (В), которые обменивающееся лицо (1) будет в зависимости от цены добавлять к количествам q_a,1, q_b,1 этих товаров, держателем которых он является, то намерения к торгу данного индивида будут вытекать из двух уравнений обмена и максимального удовлетворения


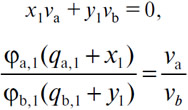
в которых можно исключить y₁, чтобы получить х₁ как функцию от p_a, или исключить x₁, чтобы получить y₁ как функцию от p_b. Полученные таким путем формулы


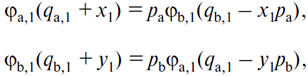
являются общими формулами, которые могут быть должным образом развернуты, чтобы выразить намерения к торгу того же самого индивида в случае обмена нескольких товаров друг на друга.

Существенно важно отметить, что первое из этих уравнений — для значений p_a, делающих отрицательный x₁ больше q_a,1, должно быть заменено уравнением x₁=—q_a,1, в этом случае y₁ будет задано уравнением y₁p_b=q_a,1; равным образом второе уравнение — для значений p_b, делающих отрицательный y₁ больше q_b,1, — должно быть заменено уравнением y₁=—q_b,1, в этом случае х₁ будет задано уравнением x₁p_a=q_b,1.

97. Эти уравнения, решенные относительно x₁ и y₁, и расположенные должным образом, чтобы удовлетворить предшествующему ограничению, примут форму:


Таким же образом, чтобы выразить намерения к торгу обменивающихся лиц (2), (3) ..., мы будем иметь


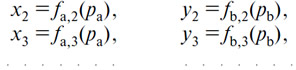
А равенство действительных предложения и спроса по каждому из двух товаров (А) и (В) будет выражаться уравнениями:


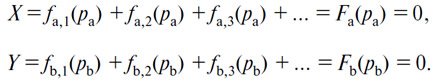
p_a можно, например, получить из первого уравнения, тогда p_b будет определено из уравнения


и это значение p_b будет с необходимостью удовлетворять второму уравнению в силу того, что мы имеем, естественно,


откуда следует, что, если F_a(p_a)=0 при определенном значении p_a, то F_b(p_b)=0 при соответствующем значении p_b.

Это решение является аналитическим. Ему можно придать геометрический вид. Сумма положительных х даст кривую спроса на (А), а сумма положительных у даст кривую спроса на (В). Из этих двух кривых спроса выводятся обе кривые предложения двух товаров, которые являются, впрочем, не чем иным, как суммами отрицательных х и у, взятых с положительным знаком. Пересечение кривых определяет текущие цены.

98. Таким будет математическое решение. А решение на рынке будет происходить следующим образом.

После того, как «выкрикнуты» две какие-либо взаимосвязанные цены p_a и p_b, то x₁, x₂, x₃ — y₁, y_2, y₃... будут определяться без каких-либо расчетов, но тем не менее в соответствии с условием максимального удовлетворения. Тем самым будут определены Х и Y Если мы будем иметь Х=0, то У также будет равен 0, а цены будут равновесными. Но обычно мы будем иметь Х<>0 и, следовательно, Y<>0. Первое неравенство может быть выражено в форме


если обозначить через D_a сумму положительных х и через О_а сумму отрицательных х, взятых с положительным знаком. Речь идет о том, чтобы сделать D_a равным О_а.

Что касается D_a, то это количество положительно при p_a=0; оно стремится к нулю, если pa растет; оно равно нулю при определенном значении р_а, заключенном между нулем и бесконечностью. Что касается О_а, то это количество равно нулю при р_а=0 и даже при некоторых положительных значениях р_а; затем оно растет, если растет р_а, но не бесконечно: оно проходит, по меньшей мере, через один максимум, затем уменьшается, если р_а продолжает расти; и оно равно нулю при р_а=∞. В этих условиях — если только D_a не становится равным нулю до того, как О_а перестало быть нулевым, случай, при котором нет решения — существует некоторое значение р_а, при котором О_а и D_a равны. Чтобы найти это значение, надо увеличивать р_а, если D_a>O_a, и уменьшать р_а, если D_aa. Мы узнаём здесь закон действительных предложения и спроса.

Примечания

* Данное обсуждение кривых спроса и предложения могло бы быть с пользой для дела дополнено доказательством (выводимым из убывания кривых полезности) следующего двоякого факта, — первого, выдвинутого в виде постулата, и второго, выведенного из первого и состоящего в том, что кривая спроса — всегда убывающая, а кривая предложения последовательно возрастает от нуля и затем убывает до нуля (в бесконечности) с ростом цены. Читатель найдет оба эти доказательства, данные для общего случая, т.е. для случая обмена некоторого числа товаров друга на друга и с участием держателей нескольких товаров, в приложении I: Геометрическая теория определения цен. Об обмене нескольких товаров друг на друга.

Источник: «Элементы чистой политической экономии», Л. Вальрас, М.: Изограф, 2000