- 71. Обстоятельство, определяющее исходную точку кривых частичного спроса: экстенсивная полезность.
- 72. Обстоятельство, определяющее наклон и конечную точку: интенсивная полезность.
- 73. Влияние имеющегося количества.
- 74. Гипотеза о единице измерения полезности или потребности. Построение кривых полезности или потребности.
- 75. Они являются кривыми действительной полезности и редкости как функции от имеющегося количества.
- 76. Обмен осуществляется с целью максимального удовлетворения потребностей.
- 77. Обмен количества ob (B) на количество da (A), после которого отношение редкости (А) к редкости (В) оказывается равным цене pa, является выгодным.
- 78, 79. Этот обмен выгоднее, чем любой другой обмен двух меньших либо больших количеств, чем ob и da.
- 80. Итак, максимальное удовлетворение имеет место, когда отношение редкостей равно цене.
- 81. Уравнение кривой спроса, выведенное из условия максимального удовлетворения.
- 82. Решение с бесконечно малыми величинами.
- 83, 84. Случай дискретных кривых потребности.
71. Проведенное нами до сих пор исследование природы факта обмена делает возможным исследование самой причины этого факта. Действительно, если цены вытекают математически из кривых спроса, то причины и исходные условия формирования и изменения кривых спроса являются также причинами и условиями формирования и изменения цен.
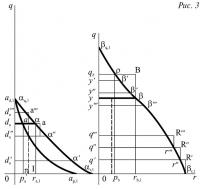
Итак, вернемся к кривым частичного спроса, например, к кривой аd,1ap,1 (рис. 1), выражающей геометрически намерения к торгу по товару (А) держателя (1) товара (В); рассмотрим сначала обстоятельство, определяющее положение точки ad,1, в которой кривая уходит от оси спроса. Длина Oad,1 представляет действительно запрошенное количество (А) данным держателем по нулевой цене, т.е. количество, которое он бы потребил, если бы товар был бесплатным. Но от чего обычно зависит это количество? От определенного вида полезности товара, которую мы будем называть экстенсивной полезностью (или полезностью по экстенсивности), так как она состоит в том, что данное благо отвечает более или менее распространенным или многочисленным потребностям в зависимости от того, что большее или меньшее число людей испытывают их и испытывают их в большей или меньшей степени, так как, одним словом, отвлекаясь от каких-либо жертв по его получению, данный товар мог бы потребляться в большем или меньшем количестве. Это первое обстоятельство является простым или абсолютным в том, что экстенсивная потребность в (А) влияет лишь на кривые спроса на (А) и что, равным образом, экстенсивная потребность в (В) влияет лишь на кривые спроса на (В). Более того, она может быть оценена, поскольку экстенсивная потребность, будучи количеством, запрашиваемым по нулевой цене, есть величина, которую можно измерить.
72. Но экстенсивная полезность не является всей полезностью, она — лишь один из ее факторов. Есть и другой фактор, который обнаружит себя, если мы теперь будем исследовать обстоятельство, определяющее наклон кривой ad,1 ap,1 и, следовательно, положение точки ap,1, в которой кривая приближается к оси цен. Наклон кривой является не чем иным, как отношением этих двух количеств: повышения цены и уменьшения спроса, вызываемым повышением. Итак, от чего обычно зависит это отношение? Это — другой вид полезности товара, которую мы будем называть интенсивной полезностью (или полезностью по интенсивности), так как она состоит в том, что этот вид богатства отвечает более или менее интенсивным или неотложным потребностям, ибо они сохраняются, несмотря на дороговизну, у более или менее большого числа людей и они более или менее сохраняются у каждого из них, потому что, одним словом, значение жертвы, связанной с их приобретением, оказывает большее или меньшее влияние на потребляемое количество товара. В отличие от первого второе обстоятельство является сложным или относительным в том смысле, что наклон кривых спроса на товар (А), равно как наклон спроса на (В), зависит одновременно от интенсивной полезности (А) и от интенсивной полезности (В). Таким образом, наклон кривых спроса, определяемый как предел отношения сокращения спроса к повышению цены, что нетрудно определить математически, дает нам лишь сложную связь между интенсивностью полезностей двух товаров.
73. Впрочем, есть еще одно обстоятельство, влияющее на наклон кривой ad,1ap,1 спроса на (А): это количество qb товара (В), находящееся в руках держателя (1) данного товара. Вообще говоря, кривые частичного спроса лежат ниже гипербол частичного количества, равно как кривые совокупного спроса — ниже гипербол совокупного количества. В зависимости от того, будет ли варьировать гипербола частичного количества, приближаясь либо удаляясь от начала координат, таким же образом будет варьировать кривая частичного спроса, как это имело бы место под воздействием вариации интенсивных полезностей. В обоих случаях рисунок дает лишь верное отражение этой необходимости.
74. Данный анализ неполон и, на первый взгляд, представляется, что невозможно продолжить его дальше в силу того обстоятельства, что абсолютная полезность по интенсивности ускользает от нас, так как в отличие от экстенсивной полезности и имеющегося количества она не находится — ни со временем, ни с пространством — в прямом и измеримом отношении. Так вот: данная трудность не является непреодолимой. Предположим, что это отношение существует, и мы сможем четко и математически учесть соответственно влияние на цены экстенсивной полезности, интенсивной полезности и имеющегося количества.
Итак, я предполагаю, что существует эталон меры интенсивности потребностей или интенсивной полезности, общий не только для сходных единиц одного и того же вида богатства, но и для различных единиц разных видов богатства. А теперь пусть даны две оси координат (рис. 3), вертикальная Oq и горизонтальная Or. На первой я наношу, начиная с 0, последовательно длины Oq', q'q", q"q''' представляющие единицы блага (В), которые держатель (1) потребил бы последовательно за определенное время, если бы он имел их в своем распоряжении. Я предполагаю, что в течение этого времени экстенсивная и интенсивная полезность является постоянной для каждого обменивающегося лица; именно это позволяет мне включать время в выражение полезности лишь имплицитно (в неявном виде). Если бы, напротив, полезность была переменной величиной в зависимости от времени, то оно должно было бы фигурировать в задаче эксплицитно и тогда бы мы перешли от экономической статики к динамике.
Но все эти последовательные единицы обладают для держателя (1) убывающей интенсивной полезностью, начиная с первой, отвечающей самой неотложной потребности и кончая последней, после потребления которой наступает насыщение; и речь идет о том, чтобы выразить это убывание математически. Если товар (В) потребляется естественным образом единицами («поединично»), как мебель или одежда, то я наношу на вторую ось, Or, и на параллельные ей прямые из точек q', q" начиная с точки 0 и с этих точек q', q"... длины (отрезки) Obr,1, q'r", q"r'''..., представляющие интенсивные полезности каждой из единиц, о которых идет речь. Я строю прямоугольники Oq'R'br,1, q'q"R"r", q"q'''R'''r'''... Таким образом я получаю кривую br,1R'r"R"r'''R'''... Эта кривая дискретна. Если бы товар (В) мог, напротив, потребляться в бесконечно малых количествах, как продукты питания, то интенсивность полезности убывала бы не только от единицы к единице, но и от первой и до последней части каждой единицы, а дискретная кривая br,1R'r"R"r'''R'''... превратилась бы в непрерывную кривую br,1r"r'''...bq,1. Таким же образом я получил бы кривую ar,1aq,1 относительно товара (А). В случае непрерывности, как, впрочем, и дискретности, я фактически полагаю, что интенсивности полезности являются убывающими начиная с интенсивности первой единицы или части единицы и кончая интенсивностью последней потребленной единицы или части единицы.
Длины Obq,1, Oaq,1 представляют экстенсивные полезности, которыми обладают товары (В) и (А) для держателя (1), или экстенсивные потребности данного держателя (1) в товарах (В) и (А). Площади Obq,1br,1, Oaq,1ar,1 представляют виртуальные (потенциальные) полезности товаров (В) и (А) для того же самого держателя, или сумму потребностей — по экстенсивности и по интенсивности — этого держателя в тех же самых товарах. Кривые ar,1aq,1, br,1bq,1 есть, таким образом, кривые полезности или потребности в товарах (А) и (В) для держателя (1). Но это не все, они обладают еще и двойной характеристикой.
75. Если мы назовем действительной полезностью общую сумму потребностей, удовлетворенных — по экстенсивности и по интенсивности — потребленным количеством товара, то кривая br,1bq,1 была бы кривой действительной полезности как функции от потребленного количества (В) для нашего индивида. Следовательно, для потребленного количества qb, представленного отрезком Oqb, действительная полезность была бы представлена площадью Oqbrbr,1. А если интенсивность последней потребности, удовлетворенной потребленным количеством товара, назвать редкостью, то кривая br,1bq,1 была бы кривой редкости как функция от потребленного количества (В) для того же индивида. Таким образом, для потребленного количества qb, представленного длиной Oqb, редкость была бы pb, представленной длиной qbr=Orb. Кривая ar,1aq,1 была бы, равным образом, кривой действительной полезности и редкости в зависимости от потребленного количества (А). Вот почему я могу назвать обе оси координат также осью редкости и осью количества. Повторю еще раз: следует принять допущение, что редкость возрастает, когда имеющееся количество убывает, и наоборот.
Алгебраически, если действительные полезности заданы в виде функции от потребленных количеств уравнениями u=Fa,1(q), u=Fb,1(q), то редкости были бы даны производными F'a,1(q), F'b,1(q). Или же, если бы редкости были даны как функция от потребленных количеств уравнениями r=φa,1(q), r=φb,1(q), то действительные полезности были бы даны определенными интегралами от 0 до q:
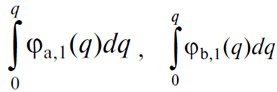
Таким образом, u и r были бы связаны как:
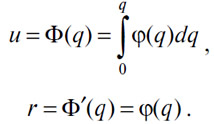
76. Если это так, то экстенсивная и интенсивная полезность (А) для держателя (1) товара (В) представлена геометрически непрерывной кривой αг,1αq,1, а алгебраически — уравнением r=φa,1(q) данной кривой; экстенсивная и интенсивная полезность (В) для него же выражена геометрически непрерывной кривой βг,1βq,1, а алгебраически — уравнением r=φb,1(q) данной кривой; впрочем, поскольку количество qb, представленное длиной Oqb, есть количество (В), которым обладает этот держатель (1), посмотрим, можем ли мы уточнить, каким будет его спрос на товар (А) по какой-либо цене.
Учитывая способ, каким мы построили наши кривые потребности, и свойства, какие мы выявили в них при их построении, можно утверждать, что если бы наш человек сохранил для себя свои qb единиц (В) с тем, чтобы их все потребить, то он удовлетворил бы общую сумму своих потребностей, представленную площадью Oqbρβr,1. Но в общем случае данный индивид поступит не так, поскольку обычно он сможет удовлетворить большую общую сумму потребностей, потребив лишь часть своего товара и обменяв излишек на некоторое количество товара (А) по текущей цене. Если, например, при цене ра (А) в (В) он удержит у себя только у единиц (В), представленных Oy, и обменяет излишек ob=qb—у, представленный yqb, на da единиц (А), представленных Oda, он сможет удовлетворить общую сумму потребностей, представленную двумя площадями Oyββr,1, Odaααr,1, сумму, которая может быть больше предыдущей. Если предположить, что он производит обмен так, чтобы удовлетворить наибольшую из возможных общую сумму потребностей, то очевидно следующее. Если дана ра, то da определяется тем условием, что совокупность обеих площадей Oyββr,1, Odaααr,1 является максимальной. Но это условие состоит в том, чтобы отношение интенсивностей ra,1 и rb,1 последних удовлетворенных потребностей было бы равно pa.
77. Предположим, что это условие выполнено, тогда мы имеем одновременно
Отсюда мы выводим, исключая pa,
или, заменяя da, ob, ra,1, rb,1 длинами Oda, qby, daa, yb, которые их представляют,
Таким образом, площади обоих прямоугольников Odaαr,1, yqbBβ равны. Но, исходя из природы кривых αr,1αq,1, βr,1βq,1 мы имеем, с одной стороны,
и, с другой,
Мы имеем, следовательно,
Таким образом, обмен количества ob (В) на количество da (А) выгоден для нашего держателя, так как получаемая им «площадь удовлетворения» больше «площади удовлетворения», от которой он отказывается. Но этого недостаточно, и надо показать, что этот же самый обмен выгоднее, чем какой угодно другой обмен меньшего или большего количества (В), чем ob, на меньшее или большее, чем da, количество (А).
78. Для этого представим себе полный обмен ob товара (В) на da (А) как состоящий из s частичных равных и последовательных обменов. Продавая последовательно s раз ob/s (B) и покупая последовательно s раз da/s (A) в соответствии с уравнением обмена
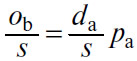
наш индивид уменьшил редкость (А) и увеличил редкость (В). Таким образом отношение этих редкостей, которое сначала было больше цены pa, стало равным данной цене. Итак, я утверждаю сначала, что в этих условиях все частичные обмены, с первого и до s-го, были выгодны, хотя и все менее и менее выгодны.
Действительно, пусть даны две длины O'da и qby’ , нанесенные на Oda и qby, одна выше точки 0, другая ниже точки qb и представляющие одна — количество da/s (A), другая — количество ob/s (B), которые были обменены во время первого частичного обмена. После того как этот первый обмен произведен, сократившееся отношение редкостей остается все еще, по допущению, больше цены, и, обозначая эти редкости через ra и rb, мы имеем
что в соответствии с предыдущим уравнением дает
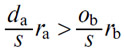
или, заменяя da/s, ob/s, ra, rb на представляющие их длины Od'a, qby', d'aα', y'β',
Но в силу природы кривых потребности мы имеем, с одной стороны,
и, с другой,
Мы можем, следовательно, с еще большим основанием утверждать, что
Таким образом, первый обмен ob/s (B) на da/s (A) был выгоден. Равным образом можно доказать, что были выгодны и дальнейшие s—2 обмена, произведенные последовательно, и сократившееся после каждого из них отношение редкостей все еще оставалось, по допущению, больше цены. Например, очевидно, что выгода уменьшалась вместе с уменьшением отношения редкостей.
А теперь пусть даны две длины dad"a и yy", нанесенные на da0 и yqb, одна ниже точки da, другая выше точки у и представляющие также одна — количество da/s (A), другая — количество ob/s (B), обмененные во время последнего частичного обмена. После того как произведен этот последний обмен, сократившееся отношение редкостей, по допущению, равно цене, и мы имеем
что в соответствии с уравнением обмена дает
или, заменяя da/s, ob/s, ra,1, rb,1 на представляющие их длины dad", yy", daα, yβ,
Но в силу природы кривых потребности мы имеем, с одной стороны,
и, с другой,
Мы имеем, следовательно,
Таким образом, последний обмен ob/s (B) на da/s (A) был все еще выгоден. Впрочем, поскольку s можно принять каким угодно большим, то очевидно, что все частичные обмены без исключения, включая последний, каким бы малым мы его ни приняли, были выгодными, хотя и все менее и менее выгодными, начиная с первого и кончая s-ым. Следовательно, не следовало ни предлагать количество (В), меньшее ob, ни запрашивать количество (А), меньшее da.
79. Таким же образом мы могли бы доказать, что не следовало предлагать количество (В), большее ob, ни запрашивать количество (А), большее da, в силу того, что все частичные обмены без исключения, включая первый, каким бы малым мы его ни приняли, все обмены, которые были бы произведены за пределами данных количеств, были бы невыгодными и все более и более невыгодными. Но, сверх того, данное доказательство полностью соответствует тому, которое мы только что дали. Действительно, продолжая уменьшать редкость (А) и увеличивать редкость (В) путем обмена некоторого количества (В) на эквивалентное количество (А), после того как был достигнут предел равенства отношения этих редкостей с ценой pa, мы приходим к неравенству
которое может быть выражено в форме
Но в силу данного выше доказательства очевидно, что в этих условиях мы приближались бы к максимуму удовлетворения, обменивая определенное количество (А) на определенное количество (В) до тех пор, пока не был бы достигнут предел
или
80. ob и oa — не больше и не меньше — будут, следовательно, теми количествами (В) и (А), которые предложит и запросит держатель (1) товара (В) по цене pa товара (А) в (В), если эти количества таковы, что мы имеем для них отношение ra,1=parb,1.
И, как общее правило: если на рынке даны два товара, то максимальное удовлетворение потребностей, или максимум действительной полезности, имеет место для каждого держателя тогда, когда отношение интенсивностей последних удовлетворенных потребностей, или отношение редкостей, равно цене. До тех пор пока это равенство не достигнуто, обменивающемуся лицу выгодно продавать товар, чья редкость меньше произведения его цены на редкость другого (товара), с тем чтобы покупать тот другой товар, чья редкость больше произведения его цены на редкость первого.
Может, таким образом, существовать выгода для обменивающегося лица в том, чтобы предложить все количество одного из двух товаров, держателем которого он является, как и не предъявлять спрос ни на какое количество другого товара. Мы вскоре вернемся к этому пункту.
81. Заменим в уравнении
ra,1, rb,1 на их значения и получим
Данное уравнение позволяет определить da как функцию от pa. Если предположить, что оно решено по отношению к первой из этих двух переменных, то оно примет форму
Это как раз уравнение кривой ad,1ap,1 спроса на (А) в (В) со стороны держателя (1). Данное уравнение было бы, следовательно, математически определенным, если бы таковыми были сами уравнения r=φa,1(q), r=φb,1(q); но поскольку они не таковы, то уравнение da=ƒa,1(a) является эмпирическим.
Таким образом решалась бы задача, состоящая в следующем; определить кривые спроса, если даны два товара (А) и (В) и кривые полезности или потребности в этих двух товарах для каждого из обменивающихся, а также количество, которым обладает каждый из держателей.
82. Было бы правильно дать формулу решения задачи, используя обычные обозначения анализа бесконечно малых.
Пусть da — запрашиваемое количество (А), ob=dapa — предлагаемое количество (В) по ценеpa товара (А) в (В) и, следовательно, qb — ob есть удерживаемое количество (В), тогда имеем
qb есть количество, которым обладает держатель.
Пусть, кроме того, u=Fa,1(q), u=Fb,1(q) уравнения, выражающие действительные полезности (А) и (В) для данного индивида в зависимости от потребленных количеств и, следовательно, Fa,1(da)+Fb,1(qb—ob) — общая действительная полезность, которую следует максимизировать. Поскольку производные функций F являются, по существу, убывающими, то искомый максимум будет иметь место для нашего индивида тогда, когда алгебраическая сумма дифференциальных приращений полезности относительно потребленных количеств каждого из двух товаров будет равна нулю, так как если допустить, что эти приращения являются неравными и имеют обратный знак, то будет выгодным запрашивать больше или меньше товара, для которого дифференциальное приращение будет большим или меньшим, предлагая больше или меньше того товара, для которого оно будет меньшим или большим. Следовательно, условие максимального удовлетворения потребностей может быть выражено уравнением
Но, с одной стороны, производные функций действительной полезности относительно потребленных количеств являются не чем иным, как редкостями, с другой, алгебраическая сумма произведений цен товаров в одном из них на дифференциалы потребленных количеств — исходя из уравнения [1] — равна нулю согласно уравнению
Таким образом, мы имеем
Я объясняю дифференцирование для читателей, мало знакомых с ним. Что касается остальных, то они сразу же поймут, что, дифференцируя одно и другое из двух выражений
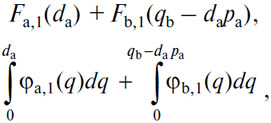
по da, получаем
или
и что корень данного производного уравнения всегда соответствует максимуму, а не минимуму в силу того, что — поскольку функции Fa,1(q) или φa,1(q), Fb,1(q) или φb,1(q) являются, по существу, убывающими — вторая производная
будет неизбежно отрицательной.
83. В нашем доказательстве предполагаются непрерывные кривые потребности; уместно рассмотреть те случаи, когда среди них есть дискретные кривые. Таких случаев три: обмен товара с непрерывной кривой на товар с дискретной кривой; обмен товара с дискретной кривой на товар с непрерывной кривой и обмен товара с дискретной кривой на товар с дискретной кривой. Но поскольку, как мы увидим ниже, выбирается товар, со стоимостью которого соотносят стоимости всех остальных товаров и с помощью которого покупают все остальные и который может и должен быть с непрерывной кривой потребности, то дозволительно ограничиться первым случаем.
Пусть даны, как всегда, βr,1βq,1 (рис. 3) — кривая полезности (В) для держателя (1) товара (В), qb — количество (В), которым он обладает.
И пусть дана кривая полезности (А) этого индивида, кривая, ступенчато проходящая через точки а и а" Поскольку товар (А) покупается только единицами («по-единично»), а pa есть его цена в (В), то товар (В) будет продаваться лишь количествами, равными pa. Если длины dad"a и dad'''a представляют последнюю купленную единицу и первую некупленную единицу (А), а длины yy" и yy''' представляют последнее проданное количество и первое непроданное количество (В), в то время как обменивающееся лицо достигло максимального удовлетворения, то мы имеем два неравенства
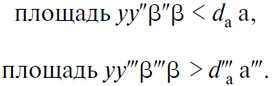
Обозначим через m" и m''' две промежуточные длины, одна между yβ и y"β", другая — между yβ и y'''β''' так, что, перемножая их на yy"=yy'''=pa, мы получим две площади, равные yy''β''β и yy'''β'''β, которые будут средними интенсивностями полезности последнего проданного количества и первого непроданного количества (В); мы можем сформулировать оба неравенства, определяющие вместе спрос на (А), da, в виде
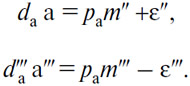
Из этих двух уравнений легко выводится
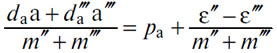
Но m"+m''' — количество, очень близкое 2yb , а (ε"+ε''')/(m"+m''') является достаточно малым количеством. Таким образом, не хватает совсем немного, чтобы иметь
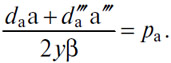
Таким образом: в случае обмена товара с непрерывной кривой потребности на товар с дискретной кривой потребности, когда имеет место максимальное удовлетворение, отношение средней интенсивности последней удовлетворенной потребности и первой неудовлетворенной потребности в купленном товаре к интенсивности последней удовлетворенной потребности в проданном товаре является примерно равным цене.
Мы говорим «примерно», так как не только произведение pa X yβ цены (A) в (В) на интенсивность последней удовлетворенной потребности в (B) может быть не равной средней интенсивностей последней удовлетворенной и первой неудовлетворенной потребности в (А), но оно может быть даже или больше, или меньше каждого из этих двух количеств. Действительно, мы имеем с необходимостью
и
но не обязательно
и, если мы имеем, напротив,
daа и d'''aа''', которое
и
но не обязательно
и, если мы имеем, напротив,
d'''aa и daа, которое >d'''aa, то они оба большеpa pa X yβ.
84. Вернемся к обоим неравенствам.
Когда pa уменьшается, то обе первые части этих неравенств уменьшаются. Первое неравенство не нарушается; но наступает момент, когда второе меняет знак и когда da увеличивается по меньшей мере на единицу. Когда pa возрастает, то обе первые части неравенств возрастают. Второе неравенство не нарушается, но наступает момент, когда первое меняет знак и когда da уменьшается по крайней мере на единицу. Кривая спроса на (А) является, таким образом, одновременно убывающей и дискретной.
Аналитически, если объявлена некоторая цена (А) в (В), pa, в зависимости от того, что наш индивид предъявит спрос на 1, 2... единиц (А), отвечающих интенсивным потребностям г1, г2.., и обеспечит себе таким путем действительные полезности (А), измеряемые теми же самыми количествами г1, г2..., то он удержит для себя количества qb—pa, qb—2pa... (В) и откажется от действительных полезностей (В), измеряемых значением определенных интегралов
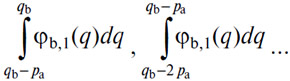
А спрос da, который обеспечит максимальное удовлетворение, будет определяться совокупностью обоих неравенств
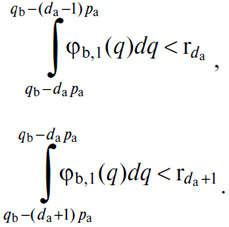
Так определяется математически da для любого значения pa и строится убывающая и дискретная кривая спроса на (А) в (В) как функция от цены.