Кривые действительных спроса и предложения

Содержание:

• 49. Факт уменьшения действительного спроса в силу повышения цены.
• 50, 51. Кривые или уравнения частичного спроса в зависимости от цены.
• 52. Кривые или уравнения полного предложения.
• 53. Кривые предложения есть одновременно кривые спроса.
• 54. Гиперболы существующего (наличного) количества.
• 55. Промежуточное положение кривых предложения между осями координат и гиперболами существующего количества.
• 56. Решение задачи обмена двух товаров между собой.
• 57. Геометрическое решение путем вписания в кривые предложения прямоугольников с взаимно обратными основаниями, высоты которых перекрестно равны их площадям.
• 58. Алгебраическое решение.
• 59. Комбинация двух решений путем построения кривых предложения в зависимости от цены.
• 60, 61. Закон действительных предложения и спроса, или установление равновесных цен.

49. Поскольку в данном случае мы считаем, что между ценой и действительным предложением имеется лишь косвенное, или опосредованное, отношение, а прямое или непосредственное отношение имеет место между ценой и действительным спросом, то нам надо исследовать именно последнее.

Возьмем для этого из числа всех держателя пшеницы. У этого индивида есть пшеница, но нет овса; он хочет сохранить некоторое количество пшеницы для себя и намерен уступить некоторое количество ее в обмен на овес для своих лошадей. Что касается соответствующих количеств, которые он сохранит и уступит, то они будут зависеть от цены овса и от количества овса, на которое он предъявит спрос с учетом его цены. Как это происходит? Посмотрим. Итак, при нулевой цене (если надо отдать ноль гектолитров пшеницы, чтобы получить 1 гектолитр овса, иначе говоря, если овес бесплатен) наш человек запросит овса вдоволь, т.е. в достаточном количестве для всех своих лошадей и даже для тех, которых он может иметь в предположении, что прокормить лошадей ничего не стоит. Впрочем, ему не нужно будет отдавать в обмен никакого количества пшеницы. При ценах, принимающих последовательно значения 1/100, 1/10, 1/5, 1/2... (если надо отдавать 1/100, 1/10, 1/5, 1/2... гектолитров пшеницы за 1 гектолитр овса), он будет все больше сокращать свой спрос. При ценах 1, 2, 5, 10. (если надо отдавать 1, 2, 5, 10. гектолитров пшеницы за 1 гектолитр овса) он сократит его еще больше. Впрочем, количество предлагаемой им в обмен пшеницы будет всегда равно произведению запрашиваемого им количества овса на цену этого овса. Наконец, при определенной более или менее высокой цене, например 100 (если надо отдать 100 гектолитров пшеницы за 1 гектолитр овса), наш человек совсем не предъявит спроса на овес, так как по этой цене он не сможет или не захочет кормить ни одной лошади. Впрочем, ясно, что в этот момент он уже не будет предлагать в обмен никакого количества пшеницы. Следовательно, из всего этого совершенно ясно, что действительный спрос на овес постоянно уменьшается по мере увеличения цены: его исходное значение составляет некоторое число при нулевой цене, а конечное значение равно нулю при определенной цене. Что касается соответствующего действительного предложения, его значение начинается с нуля, увеличивается, достигает по меньшей мере одного максимума, затем уменьшается и возвращается к нулю.


50. Все держатели пшеницы, и не только все держатели пшеницы, с одной стороны, но и все держатели овса, с другой, имеют не одинаковые намерения, а аналогичные. И, вообще говоря, каждый держатель какого-либо товара, направляющийся на рынок, чтобы обменять на нем некоторое количество этого товара на некоторое количество другого товара, несет с собой намерения к торгу, потенциальные либо действительные, которые можно определить строгим образом.

Каждый держатель (1) количества q_b товара (В), скажем мы, переходя к алгебраическим обозначениям, направляющийся на рынок, чтобы обменять там некоторое количество o_b этого товара, которое он будет предлагать, на некоторое количество d_a товара (А), на которое он предъявит спрос, в соответствии с уравнением


вернется оттуда с количеством d_a товара (А) и количеством


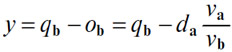
товара (В). Так или иначе, между количествами q_b, v_a/v_b или p_a, d_a и y всегда сохраняется отношение


Наш человек знает, что такое q_b. Он не знает, пока не пришел на рынок, каким будет v_a/v_b или p_a; но он уверен, что узнает это, как только придет, и, зная величину p_a, он должен будет сразу же принять для себя определенное значение d_a, из которого последует, в конечном счете, определенное значение y в силу указанного выше уравнения.


Если наш человек сам идет на рынок, он может оставить свои намерения к торгу в потенциальном, а не в действительном состоянии, т. е. определять свой спрос d_a лишь после того, как известна цена p_a. Даже в этом случае его намерения существуют. Но если, например, что-то мешает ему лично пойти на рынок либо по той или иной причине он должен дать поручение другу или распоряжения маклеру, то он должен будет предусмотреть все возможные значения p_a, от нуля до бесконечности, и определить отсюда все соответствующие значения d_a, выражая их каким-либо образом. Но тот, кто хоть немного привычен к расчетам, знает, что есть два способа выразить это математически.

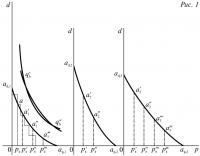
51. Даны две оси координат (рис. 1), горизонтальная ось цен O_p и вертикальная ось спроса O_d. На одну, начиная с начала координат 0, я наношу длины Op'_a, Op"_a..., соответствующие различным возможным ценам овса, выраженным в пшенице, или (А) в (В). На другую, также с начала координат 0, я наношу длину Oa_d,1, соответствующую количеству овса или (А), на которое предъявит спрос наш держатель пшеницы, или (В) при нулевой цене; и на параллельных оси спроса линиях, начинающихся в точках p'_a, p"_a..., я наношу из этих точек длины p'_a a'₁, p"_a, a"₁..., соответствующие соответственно тем количествам овса или (А), которые будут запрошены при соответствующих ценах p'_a, p"_a... Длина Oa_p,1 будет представлять цену, при которой наш держатель пшеницы или (В) не предъявит более никакого спроса на овес или (А).

Итак, намерения к торгу держателя (1) товара (В) выражены либо геометрически кривой a_d,1, a_p,1, проходящей через точки a_d,1, a'₁, a"₁...a_p,1, либо алгебраически уравнением d_a=ƒ_a,1 (p_a) данной кривой. Кривая a_d,1 a_p,1 и уравнение d_a=ƒ_a,1 (p_a) являются эмпирическими. Таким же образом мы получим кривые a_d,2, a_p,2, a_d,3, a_p,3... или их уравнения d_a=ƒ_a,2 (p_a), d_a=ƒ_a,3 (p_a), выражающие геометрически либо алгебраически намерения к торгу всех остальных держателей (2), (3)... товара (В).


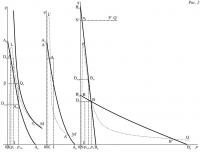
52. Если теперь мы сложим, так сказать, все эти частичные кривые a_d,1a_p,1, a_d,2a_p,2, a_d,3a_p,3 друг с другом, складывая все ординаты по одной и той же абсциссе, мы получим полную кривую A_dA_p (рис. 2), выражающую геометрически намерения к торгу всех держателей (В). Или если мы сложим все частичные уравнения, то получим полное уравнение


выражающее алгебраически те же самые намерения. Это — кривая или уравнение спроса на (А), выраженное в (В) как функция от цены (В) в (А).

Ничто не указывает на то, что частичные кривые или уравнения a_d,1a_p,1, d_a=ƒ_a,1 (p_a) и остальные являются непрерывными, т.е. что бесконечно малое увеличение p_a приводит к бесконечно малому уменьшению d_a. Напротив, эти функции часто будут прерывистыми (дискретными). Что касается овса, например, очевидно, что наш первый держатель пшеницы будет сокращать свой спрос не по мере роста цены, а в некотором роде скачками — каждый раз, когда он решит держать в конюшне на одну лошадь меньше. В итоге его частичная кривая спроса будет выглядеть в действительности ступенчатой, проходя через точку a (рис. 1). Так же будет и с остальными. И однако, полная кривая A_dA_p (рис. 2) может — в силу так называемого закона больших чисел — рассматриваться как в значительной степени непрерывная. Действительно, когда произойдет очень малое увеличение цены, то из большого числа по меньшей мере один держатель (В) подойдет к пределу, вынуждающему его освободиться от одной лошади, и произойдет также очень алое уменьшение общего спроса.


53. В этих условиях кривая A_dA_p дает, следовательно, действительно запрашиваемое количество (А) в зависимости от цены (А). Например, при цене р_a,m , представленной абсциссой Op_a,m точки A_m, действительным спросом является D_a,m по цене p_a,m, представленный ординатой OD_a,m той же точки Am. Впрочем, когда действительный спрос на (А) в (В) будет D_a,m по цене p_a,m, то действительное предложение (В) в обмен на (А) будет тем самым O_b,m=D_a,mp_a,m, что представлено прямоугольником OD_a,mA_mp_a,m с координатами OD_a,m, Op_a,m по его площади. Таким образом, кривая A_dA_p представляет одновременно спрос на (А) и предложение (В) в зависимости от цены (А) в (В). Равным образом кривая B_dB_p представляет одновременно спрос на (В) и предложение (А) в зависимости от цены (В) в (А).

54. Пусть дано совокупное количество (В), имеющееся на рынке в руках держателей этого товара, и дана кривая, проходящая через точку Q_b равносторонней приближающейся к своим асимптотам гиперболы, уравнение которой xy=Q_b. Продолжим линию p_a,mA_m до пересечения с этой гиперболой в точке Q_b и проведем прямую, параллельную оси х или цен b Qm_b. Площадь Q_b прямоугольника ObQ_bp_a,m представляет совокупное количество (В), принесенное на рынок.; площадь Dampam прямоугольника OD_a,mA_mp_a,m представляет часть, которая будет уступлена в обмен на (А) по цене pa m; и, следовательно, площадь Y прямоугольника D_a,mbQ_bA_m, т.е. Q_b — D_a,mp_a,m, представляет часть, которая будет унесена обратно с рынка и сохранена держателями при той же цене p_a,m. Итак, в любом случае между количествами Q_b, p_a, D_a и Y у нас всегда будет отношение


Таким образом, xy=Q_b, или кривая, проходящая через точку Q_b, будучи гиперболой наличного количества (В), A_dA_p есть кривая раздела этого количества на часть, подлежащую обмену на (А), и часть, оставляемую у себя, в зависимости от цен (А) и (В). Естественно, то же отношение мы найдем между кривой B_dB_p и гиперболой наличного количества (А), уравнение которого будет xy=Q_a.

55. Кривые спроса замкнуты, следовательно, в гиперболах количества. Можно также сказать, что обычно эти кривые пересекают оси координат и не являются их асимптотами.

Обычно они пересекают ось спроса. Действительно, количество какого-либо товара, запрашиваемого индивидом по нулевой цене, является в общем случае конечным. Если бы овес был бесплатным, то некоторые люди содержали бы десятки или сотни лошадей, но не бесконечное количество, и не предъявляли бы спрос на неограниченное количество овса. Будучи суммой конечных количеств, общая сумма спроса была бы и сама конечной.

Эти кривые пересекают обычно и ось цен. Действительно, можно, в общем, предположить, что имеется достаточно высокая, но не бесконечная цена, по которой уже никто не предъявляет спрос на какой-либо товар даже в бесконечно малом количестве. И однако, в целом, в этом отношении нельзя утверждать ничего абсолютного. Вполне можно представить случай, когда товар (В) предлагается по любой цене либо в полном объеме, либо частично и когда, следовательно, кривая спроса A_dA_p совпадает полностью или частично с гиперболой, проходящей через Q_b, или с некоторой другой внутренней гиперболой. Вот почему, дабы не забегать вперед, мы будем считать, что кривые спроса могут занимать любое положение между осями координат и гиперболами наличного количества.

56. Нам известна природа прямого и непосредственного отношения, связывающего действительный спрос на товар с его ценой в другом товаре, и мы можем дать математическое выражение этого отношения.

Так, для товара (А) это отношение будет выражаться геометрически кривой A_dA_p или алгебраически уравнением данной кривой


Для товара (В) оно будет выражаться геометрически кривой B_dB_p или алгебраически уравнением данной кривой


Более того, нам известна также природа косвенного и опосредованного отношения, существующего между действительным предложением одного товара в обмен на другой и ценой последнего товара в первом, и мы можем также представить математическое выражение данного отношения.

Для товара (А) отношение, о котором идет речь, будет выражаться геометрически рядом прямоугольников, вписанных в кривую B_dB_p, или алгебраически уравнением


Для товара (В) оно будет выражаться геометрически рядом прямоугольников, вписанных в кривую A_dA_p, или алгебраически уравнением


Впрочем, нет ничего проще из последних выражений вывести те, которые относятся к отношению, связывающему действительное предложение каждого товара с его собственной ценой в другом товаре. Достаточно всего лишь заменить в первых двух уравнениях цену p_b на 1/p_a и цену pa на 1/p_b в силу соотношения p_ap_b=1.

Тогда мы получим


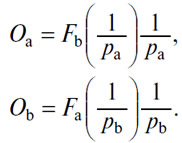
Имея все эти элементы, мы в состоянии математически решить общую задачу обмена двух товаров друг на друга, состоящую в следующем: необходимо определить соответствующие равновесные цены, если даны два товара (А) и (В) и кривые спроса на эти два товара, один в обмен на другой, или уравнения данных кривых.

57. Геометрически задача состоит в том, чтобы вписать в обе кривые A_dA_p, B_dB_p два прямоугольника OD_aAp_a, OD_bBp_b с взаимно обратными основаниями так, чтобы высота одного OD_a была равна площади другого Od_b X Op_b и чтобы, наоборот, высота второго OD_b была равна площади первого OD_a X Op_a. Основания этих двух прямоугольников — Op_a, Op_b — будут представлять равновесные цены, так как при данных соответствующих ценах спрос на (А), представленный высотой OD_a, будет равен предложению (А), представленному площадью OD_b X Op_b, а спрос на (В), представленный высотой ODb, будет равен предложению (В), представленному площадью OD_a X Op_a.

Выражение «высоты, равные площадям», которое я использовал, не однородно. Но в данном случае эта однородность не является необходимой в силу того, что условие обратной зависимости оснований предполагает определение общей единицы OI, использованной для построения обеих кривых. Однако если есть желание выявить ее, то можно было бы сказать, что высота каждого прямоугольника должна содержать единицу длины столько раз, сколько единиц площади содержит площадь другого; или, говоря иначе, что площадь каждого прямоугольника должна быть равна площади такого прямоугольника, который построен по высоте другого на основании, равном единице. Впрочем, в данных задачи само собой разумеется, что основания обоих прямоугольников равны обратным отношениям высот и прямым отношениям соответствующих площадей.

58. Алгебраически задача состоит в нахождении двух корней p_a, p_b двух уравнений


или двух корней p_a, p_b двух уравнений


или, наконец, двух корней двух уравнений


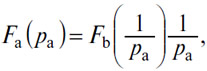
выражающего, что D_a = O_a, и


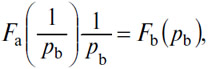
выражающего, что O_b = D_b.

59. Оба метода могут к тому же быть объединены в один. У нас уже есть кривые


это кривые A_dA_p, B_dB_p. Построим кривые


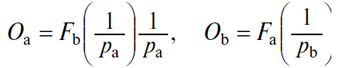
это будут кривые KLM, NPQ, пересечение которых с первыми кривыми в точках А и В даст как раз прямоугольники, о которых шла речь выше.

Нетрудно убедиться в том, что такое эти кривые KLM, NPQ, изображенные на рисунке пунктиром, и каким образом они построены.

Первая, KLM, является кривой предложения (А), но не той, что совпадает с кривой спроса на товар (В) и дает нам предложение (А) через площади прямоугольников координат в зависимости от p_b, а отличной от нее кривой, дающей это предложение (А) через длины ординат в зависимости от p_a.

Она начинается с нуля при бесконечно большой цене (А), выраженной в (В), соответствующей бесконечно малой цене (В) в (А), т.е. она асимптотична оси цен. Она поднимается по мере приближения к началу координат при убывающих ценах (А) в (В), соответствующих возрастающим ценам (В) в (А). Она достигает максимума L, чья абсцисса представляет цену (А) в (В), обратную цене (В) в (А) p_b,m, представленной абсциссой Op_b,m точки B_m, для которой прямоугольник, вписанный в B_dB_p, является максимальным. Затем она идет вниз, еще более приближаясь к началу координат, и возвращается к нулю при цене (А) в (В), представленной ОК, обратной по величине цене (В) в (А), представленной абсциссой OB_p точки B_p, в которой кривая B_dB_p пересекает ось цен.

Равным образом вторая кривая, NPQ, является кривой предложения (B), но не той, что совпадает с кривой спроса на товар (A) и дает нам предложение (B) через площади прямоугольников координат в зависимости от p_a, а отличной от нее кривой, дающей это предложение (B) через длины ординат в зависимости от p_b.

Она начинается с нуля при бесконечно большой цене (B), выраженной в (A), соответствующей бесконечно малой цене (A) в (B), т. е. она асимптотична оси цен. Она поднимается по мере приближения к началу координат при убывающих ценах (B) в (A), соответствующих возрастающим ценам (A) в (B). Она достигает максимума P, чья абсцисса представляет цену (B) в (A), обратную цене (A) в (B) p_a,m, представленной абсциссой Op_a,m точки A_m, для которой прямоугольник, вписанный в A_dA_p, является максимальным. Затем она идет вниз, еще более приближаясь к началу координат, и возвращается к нулю при цене (B) в (A), представленной ON, обратной по величине цене (A) в (B), представленной абсциссой OA_p точки A_p, в которой кривая A_dA_p пересекает ось цен.

Разумеется, данная форма кривых KLM, NPQ соотносится в принципе с формой кривых B_dB_p, A_dA_p. Если предположить, что последние выглядят иначе, то и первые будут полностью иными. Как бы там ни было, при избранных нами данных кривая B_dB_p идет вниз и, пройдя точку максимума B_m, пересекает пунктирную кривую NPQ в тот момент, когда последняя идет вверх от нуля к своему максимуму P; и, следовательно, кривая A_dA_p также пересекает пунктирную кривую KLM на нисходящем участке до прохождения максимальной точки A_m в тот момент, когда последняя кривая идет вниз от своего максимума L до нуля.

60. Итак, учитывая данное расположение, очевидно, что если в точке А встречаются две кривые A_dA_p и KLM, то справа или слева от этой точки, напротив, кривая A_dA_p ниже или выше кривой KLM; если же в точке В встречаются две кривые B_dB_p и NQP, то справа или слева от этой точки, напротив, кривая BdBp ниже или выше кривой NQP.

Таким образом, поскольку, по допущению, цены p_a=1/μ и p_b=μ являются такими, при которых D_a=O_a и O_b=D_b, то для всех цен (А) в (В), превышающих pa, соответствующих ценам (В) в (А), уступающих (меньших) pb, мы будем иметь одновременно O_a>D_a и D_b>O_b. В первом случае к равновесной цене можно было бы прийти лишь через повышение p_b, что было бы понижением p_a. Во втором случае к этому можно прийти лишь через повышение p_a, что было бы понижением p_b.

Все это приводит нас к формулированию закона действительных предложения и спроса, или закона установления равновесных цен, для случая обмена двух товаров друг на друга в следующих терминах: если даны два товара, то чтобы имелось рыночное равновесие по отношению к ним, или стационарная цена одного товара в другом, необходимо и достаточно, чтобы действительный спрос на каждый из двух товаров был равен его действительному предложению. Если это равенство не существует, то, чтобы прийти к равновесной цене, необходимо повышение цены товара, действительный спрос на который выше его действительного предложения, и понижение цены того товара, действительное предложение которого выше действительного спроса на него.

Закон таков, что мы могли бы испытать искушение сформулировать его сразу же после исследования биржевого рынка, но было необходимо строгое доказательство.

61. Сейчас мы ясно видим, что представляет собой механизм конкуренции на рынке; это — практическое решение путем повышения и понижения цен задачи обмена, чье теоретическое и математическое решение мы дали выше. Впрочем, надо понимать, что в наше намерение нисколько не входила подмена одного решения другим. Практическое решение является столь быстрым и надежным, что нельзя желать ничего лучшего. Можно наблюдать, как на больших рынках, функционирующих даже без маклеров и «крикунов», текущая равновесная цена определяется в несколько минут и по этой цене за половину или три четверти часа обмениваются значительные количества товара. Теоретическое решение, напротив, было бы почти во всех случаях совершенно невозможным на практике. Вот почему говорить о трудности нахождения кривых обмена или их уравнений значило бы выдвигать против нас необоснованное возражение. Что же касается пользы построения в некоторых случаях кривой спроса или предложения — полностью или частично — для определенного товара, а также возможности или невозможности сделать это, то данный вопрос мы целиком оставляем на будущее. В данный момент мы исследуем задачу обмена в общем, и чистое и простое представление о кривых обмена для нас и достаточно, и необходимо.