Установление стоимости биметаллического эталона

Содержание:

• 284. При монометаллической системе имеется 3 уравнения для нахождения 3 неизвестных задачи определения стоимости денег; при биметаллической системе для нахождения 6 неизвестных имеется только 5 уравнений; надо ввести шестое. Это шестое уравнение может быть получено путем законодательно фиксированного отношения стоимости золотых и серебряных денег.
• 285. Если это соотношение зафиксировано, то отношение стоимости золота как товара к стоимости серебра как товара стремится к нему через превращение каждого из двух металлов из денег в товар и из товара — в деньги.
• 286. Уравнения биметаллизма.
• 287. Геометрическое решение уравнений биметаллизма. Закон установления общей и одинаковой цены двух товаров-денег.
• 288. Увеличение и уменьшение количества каждого металла.
• 289. Последствия прекращения и возобновления выпуска серебряных денег.

284. Спор между сторонниками монометаллизма и биметаллизма поразительным образом доказывает, что, отказываясь применить к исследованию количественных по существу фактов единственный подходящий метод, мы оставляем неясными и нерешенными — в этих вопросах — ключевые пункты, которые при желании можно было бы выяснить с математической строгостью.
В предыдущем уроке я показал, что если в качестве денег используется только один товар (A), то для определения трех неизвестных:

• 1) количества (A), остающегося в товарной форме;
• 2) количества (A), ставшего деньгами;
• 3) общей цены (A) как товара и (A) как денег, выраженной в каком-либо другом товаре имеется три уравнения, выражающих:

• 1) что сумма количеств (A) товара и (A) денег равна совокупному количеству (A);
• 2) как цена (A) товара следует из количества (A) товара;
• 3) как цена (A) денег следует из количества (A) денег.

Если же теперь в качестве денег будут использоваться параллельно два товара (A) и (O), то для определения 6 неизвестных, каковыми являются:

• 1) количество (А) товара;
• 2) количество (А) денег;
• 3) количество (О) товара;
• 4) количество (О) денег;
• 5) цена (А) товара и денег;
• 6) цена (О) товара и денег —

у нас будет только 5 уравнений, выражающих:

• 1) что сумма количеств (A) товара и (A) денег равна совокупному количеству (A);
• 2) что сумма количеств (O) товара и (O) денег равна совокупному количеству (O);
• 3) как цена (A) товара следует из количества (A) товара;
• 4) как цена (O) товара следует из количества (O) товара;
• 5) как цены (A) денег и (O) денег вместе обусловливаются количествами (A) и (O), играющими роль денег.

Если бы в качестве денег параллельно использовались 3 товара, то для нахождения 9 неизвестных было бы только 7 уравнений.

Если бы использовались 4 товара, то для определения 12 неизвестных было бы только 9 уравнений. И так далее.

Таким образом, в условиях единственного эталона задача полностью определена и разрешается сама собой на рынке при помощи механизма свободной конкуренции. Законодателю остается лишь указать товар-деньги (A), позволить преобразовывать деньги в товар, когда цена (A) товара выше цены (А) денег, и преобразовывать самому, как только его об этом попросят, товар в деньги, когда стоимость (A) денег выше стоимости (A) товара.

Напротив, в случае двойного эталона задача определена не полностью и законодатель может вмешаться, чтобы по своей воле определить одну из шести неизвестных или чтобы тем или иным способом ввести шестое уравнение. Он может, к примеру, произвольно определить количество (A) денег, или количество (O) денег, или отношение первого количества ко второму. В этом последнем случае будет иметь место биметаллизм с постоянным соотношением количеств^*. Или же он может произвольно задать цену (A) денег или цену (O) денег или отношение первой цены ко второй. В последнем случае мы имеем биметаллизм с постоянным соотношением стоимостей. Если законодатель определяет количество, то на рынке стоимость определится сама собой. Если же он определяет стоимость, то тогда количество определится само собой через механизм свободной конкуренции.

285. Предположим, что принято последнее решение и соотношение стоимости золотых и серебряных денег зафиксировано на уровне 15 1/2, как того требуют сторонники биметаллизма. Вот как установятся тогда соответствующие количества золота и серебра, превращенных в деньги или нет. Если отношение стоимости золота как товара к стоимости серебра как товара будет выше 15 1/2, то на изготовление драгоценностей и утвари пойдет не только все добываемое в шахтах золото, но и, более того, часть золотых денег будет превращена в товарное золото; в то же самое время не только все вновь добытое серебро станет деньгами, но и, кроме того, часть товарного серебра будет превращена в серебряные деньги. Таким образом, количество золотых денег уменьшится, а серебряных — увеличится. Количество же товарного золота увеличится, а товарного серебра — уменьшится; так будет происходить до тех пор, пока соотношение стоимости товарного золота и стоимости товарного серебра не снизится до 15 1/2. Если же отношение стоимости товарного золота к стоимости товарного серебра будет ниже 15 1/2, то произойдут обратные явления. Количество золотых денег увеличится; количество серебряных денег уменьшится. Количество товарного золота снизится, а товарного серебра — вырастет; так будет происходить до тех пор, пока соотношение стоимости товарного золота и стоимости товарного серебра не поднимется до 15 1/2.


Из этих объяснений следует, что сторонники монометаллизма заблуждаются, когда категорично утверждают, что обещать незыблемость 15 1/2 — значит обещать невозможное. Такая незыблемость — в определенных пределах — возможна без нарушения свободной конкуренции. Но отсюда следует и то, что сторонники биметаллизма сами заблуждаются, полагая, что соотношение 15 1/2 — будучи установленным законодательно как соотношение стоимости золотых и стоимости серебряных денег — в силу одного этого факта становится раз и навсегда как бы естественным отношением стоимости товарного золота к стоимости товарного серебра. Товар может быть также деньгами, но, становясь деньгами, он остается тем не менее товаром, а как таковой он имеет цену, определяемую законом предложения и спроса. Данная цена — в виде исключения и на короткое время — может быть то выше, то ниже цены денег, и, следовательно, добытчику металла может быть выгодным доставлять его то на рынок, то на Монетный двор, а меняле — то переплавлять монеты (экю), то отдавать слитки для чеканки монет. Именно это и видим мы каждый день и при системе единого эталона, и при системе двойного эталона. Разумеется, в этом последнем случае законодательно навязанное соотношение обмена металлических денег в 15 1/2 переносится на товарный металл при помощи механизма свободной конкуренции, но не сразу и не навсегда. Если отношение стоимости товарного золота к стоимости товарного серебра выше 15 1/2, то оно понижается только лишь путем демонетизации золота (переплавки части золотых монет) и до тех пор, пока есть золото для демонетизации; после чего это соотношение становится равным 16, 17, 18... Если данное соотношение ниже 15 1/2, оно повышается только лишь путем демонетизации серебра (переплавки части серебряных монет) и до тех пор, пока есть серебро для демонетизации, после чего указанное соотношение становится равным 15, 14, 13. Сторонники биметаллизма говорят нам, справедливо или нет, что нынешнее снижение стоимости серебра вызвано действием закона, а не действием сил природы, но они не могут всерьез думать, что есть гарантии, при которых силы природы никогда не проявят себя. Итак, важно знать следующее: в условиях биметаллической системы может произойти такое увеличение количества серебра, что это приведет к демонетизации (переплавке в товарную форму) всего золота и вынудит нас совершать крупные платежи весьма тяжелыми суммами [по весу серебряных денег — Прим. перев.]; или же такое увеличение количества золота, что это приведет к демонетизации (переплавке в товарную форму) всего серебра и вынудит нас совершать мелкие платежи крохотными монетками; иными словами, система двойного эталона на базе законодательно установленного курса в 15 1/2 , независимо от того, носит она локальный либо универсальный характер, всегда является, в конечном счете, системой альтернативного эталона, при которой обесценивающийся металл в большей или меньшей степени вытесняет из обращения металл, стоимость которого растет.


Такова теория, которую нам надо разработать математически.

286. Геометрическое построение, данное в уроке 30, соответствует алгебраическому решению трех уравнений


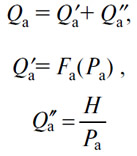
из которых находятся три неизвестные P_a, Q'_a и Q''_a. Таким образом, в этом случае имеются 3 уравнения для нахождения 3 неизвестных.

Пусть теперь в качестве денег выступают одновременно два товара — (A) и (O); пусть Q_a и Q_o — их совокупные количества, Q'_a и Q'_o — их количества, остающиеся в форме товаров, Q'_a и Q''_o — их количества, используемые в качестве денег. Пусть P_a и P_o обозначают их цену в некотором третьем товаре (В). Для определения этих 6 неизвестных имеем 5 уравнений:


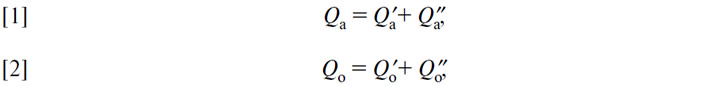
выражающие, что совокупные количества (A) и (O) равны суммам количеств (A) товара и (A) денег и количеств (О) товара и (O) денег;


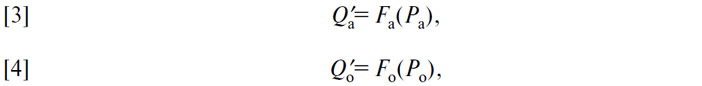
выражающие, как цены (А) товара и (O) товара связаны с количествами (А) товара и (O) товара;



означающее, что количество денег (А) и количество денег (О) дают вместе желаемый объем наличности.

И, если угодно, чтобы закончить постановку задачи, можно ввести уравнение


фиксирующее соотношение стоимостей P_o и P_a. Именно это и происходит, когда государство объявляет, что в платежах одна единица (O) и ю единиц (A) эквивалентны^**.

287. Подставляя значение P_o из уравнения [6] в уравнения [4] и [5], а затем значения Q'_a и Q'_o полученные из уравнения 3 и измененного уравнения 4, в уравнения 1 и 2, получаем


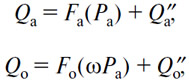
или


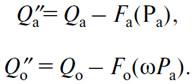
Подставляя эти значения Q''_a и Q''_o измененное уравнение 5, получаем


или


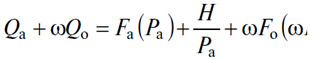
уравнение, из которого можно вывести P_a и которое допускает очень простое геометрическое решение.

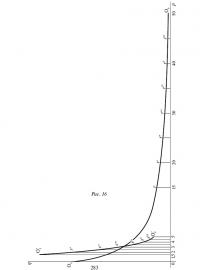
Отложим (Рис. 16) в прямоугольной системе координат цены по оси абсцисс O_p и количества по оси ординат O_q.

Рассмотрим проходящую через точку H (Рис. 15) кривую — равнобочную гиперболу, асимпототически стремящуюся к осям координат и описываемую уравнением


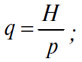
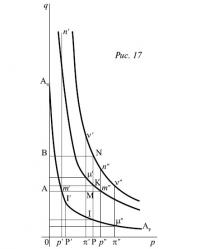
возьмем кривую A_qA_p, связывающую цену (A) товара, выраженную в (B), с количеством (Рис. 17), ее уравнение можно записать в виде


и рассмотрим кривую O_qO_p (Рис. 16), связывающую цену (О) товара, выраженную в (B), с количеством, ее уравнение


Я преобразую эту последнюю кривую следующим образом. От начала координат наношу на горизонтальной оси абсциссы 1.5, 2, 2.5, 3..., равные 1/ω абсцисс 15, 20, 25, 30. (ω на рисунке равен 10). Из этих точек на оси абсцисс провожу вверх прямые, параллельные вертикальной оси, и наношу на них ординаты O'_q, s', s'', s'''…, равные произведениям ω на ординаты r, r', r'', r'''… Так получается кривая O_qO_p, чье уравнение


Это преобразование тут же станет понятным, если принять во внимание то обстоятельство, что в системе с постоянным соотношением стоимостей (A) и (O) одна единица (O) может быть заменена w единицами (A), каждая из которых стоит в w раз меньше. Кривая O'_qO'_p тем самым оказывается, в некотором смысле, кривой цены (O) в виде (A).

После этих предварительных замечаний найдем геометрическое решение уравнения


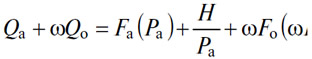
следующим образом. Для всех значений абсцисс добавим к ординатам кривой, проходящей через точку H (рис.15), ординаты кривой A_qA_p (Рис. 17), получая таким образом кривую μ'Km'', характеризующуюся уравнением


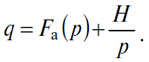
Затем для всех абсцисс я добавляю к ординатам кривой O'_qO'_p (рис.16) ординаты кривой μ'Km'' (Рис. 17), получая кривую n'Nn'', описываемую уравнением


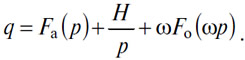
Теперь совокупное количество (A), равное Q_a, соответствует расстоянию OA на графике, а совокупное количество (О), взятое ω раз, ωQ_o, соответствует расстоянию AB. Проведя горизонтальную линию BN до пересечения с верхней кривой и опустив из точки N перпендикуляр NP, получим абсциссу OP, показывающую цену P_a товара и денег (A), соответствующую количеству Q_a. Вдобавок к этому, расстояния PI и IM представляют соответствующие количества Q'_a и Q''_a товара (A) и денег (A), при этом не происходит никакого преобразования товара (A) в деньги (A), ни наоборот. Кроме того, абсцисса 50=ωОР (Рис. 16) показывает цену P_o товара и денег (O), соответствующую количеству Q_o. Вдобавок к этому, расстояния NK и KM (Рис. 17) представляют взятые ю раз количества Q'_o и Q''_o товара (O) и денег (O) соответственно, при этом также не происходит никакого преобразования товара (O) в деньги (O), ни наоборот. Можно было бы доказать, точно так же, как мы это делали в случае единого денежного эталона, что если бы мы разделили количества Q_a и Q_o не на Q'_a и Q''_a и Q'_o и Q''_o, как сделали это выше, а на произвольные и разные доли, то для двух случаев мы снова получили бы, что (A) как товар преобразуется в (A) деньги, или же наоборот, и что (O) как товар превращается в (O) деньги, или наоборот. Для этого доказательства было бы достаточно предположить, что расстояние PN делится на три части иначе, чем на PI, IK и KN, и что это деление по-другому разбивает расстояние между осью O_p и тремя кривыми A_qA_p, μ'Km'' и v'Nn''. Я воздержусь от повторения этого доказательства в целях краткости изложения и во избежание усложнения рисунка, который еще понадобится мне для другого доказательства.

Итак: В случае двух одновременно действующих стандартов, как и в случае единого эталона, единая и равная, выраженная в некотором третьем товаре цена каждого из двух товаров-денег в качестве товара и в качестве денег устанавливается путем дополнительной чеканки монет или демонетизации (превращения денег в слитки) в зависимости от того, оказалась ли цена денег выше цены товара, или наоборот.

288. Три кривые: H, A_qA_p, O_qO_p, расстояния OA и AB (Рис. 15, 16, 17) и соотношение ω, являясь, таким образом, элементами установления цены обоих товаров-денег и определения соответствующих количеств товаров и денег, являются также, в силу этого же обстоятельства, элементами изменения этих цен и этих количеств. И на этот раз, чтобы учесть все явления изменения цены двух товаров-денег и соответствующих количеств товаров и денег, было бы достаточно последовательно рассмотреть последствия смещения кривых H, A_qA_p, O_qO_p и последствия изменений расстояний OA, AB и пропорции ю. Сравнивая результаты этого исследования для случая двух одновременно действующих стандартов с результатами аналогичного анализа для случая единого эталона, можно было бы с полным знанием дела говорить о сравнительных достоинствах монометаллизма и биметаллизма с точки зрения наибольшей устойчивости стоимости счетного товара и денег. Именно этим мы займемся в следующем уроке, но сначала изучим здесь последствия изменений расстояний OA и AB, соответствующих изменениям количеств Q_a и Q_o.

Предположим сперва, что при постоянстве величины Q_a, представленной расстоянием OA, величина Q_o, соответствующая на графике MN/ω, возрастает до количества, обозначенного m'n'/ω, или снижается до количества, обозначенного m''n''/ω. Из рис. 17 видно, что в первом случае все совокупное количество серебра p'm' будет товарным, а денежное обращение будет обслуживаться исключительно золотом, тогда как во втором все имеющееся золото m''n''/ω будет товарным, а обращение будет обслуживаться исключительно серебром. Из рисунка видно также, что если Qo увеличится до количества, превосходящего m''n''/ω, или уменьшится до количества, меньшего, чем m''n''/ω, причем цена серебра будет оставаться равной p' или p'', а цена золота станет в первом случае ниже p', а во втором — выше p'', то отношение стоимости товарного золота к стоимости товарного серебра в первом случае будет меньше ω, а во втором — больше.

Предположим теперь, что Q_o, представленное MN/ω=μ'v'/ω=μ''v''/ω, остается постоянным, а Q_a, соответствующее расстоянию PM, возрастает до количества π'μ' или уменьшается до количества π''μ''. Из рисунка видно, что в первом случае все количество золота μ'v'/ω будет товарным и что денежное обращение будет обслуживаться исключительно серебром, тогда как во втором все имеющееся серебро π''μ'' будет товарным, а обращение будет обслуживаться исключительно золотом. Из рисунка видно также, что если Q_a будет увеличиваться до количества, превосходящего π'μ', или уменьшаться до количества, меньшего, чем μ''v''/ω, причем цена золота будет оставаться равной π' или π'', а цена серебра станет в первом случае — ниже π', а во втором — выше π'', то отношение стоимости товарного золота к стоимости товарного серебра в первом случае будет больше ω, а во втором — меньше.

Этого, я полагаю, достаточно, чтобы показать, до какой степени поверхностными были до сих пор исследования проблемы монометаллизма и биметаллизма, и чтобы наметить верный путь для тех умов, которые захотели бы более глубоко изучить этот вопрос. Совершенно необходимо, чтобы сторонники монометаллизма прекратили на любые предложения сторонников биметаллизма возражать, что «поддержание постоянного соотношения между стоимостью золота и стоимостью серебра — задача для государства столь же трудная, что и поддержание такого соотношения между стоимостями пшеницы и ржи»^***. Государству отнюдь не сложно поддерживать постоянное соотношение между стоимостью золотых и стоимостью серебряных денег, и если такое соотношение установлено, то в тенденции оно будет косвенно распространяться и на соотношение стоимостей товарного золота и товарного серебра. Но и сторонники биметаллизма должны перестать отрицать, что «денежный металл может менять свою стоимость, изменяя форму», и утверждать, что «между стоимостями металла в слитках, металла в качестве счетного товара и металла, используемого в ювелирных целях, существует постоянное тождество»^****. Такое тождество стоимостей металла в качестве товара и металла в качестве денег далеко не постоянно, оно поддерживается только за счет дополнительной чеканки монеты или демонетизации металла и прекращает иметь место, когда более нет металла для демонетизации.

289. Формулировки, использованные в настоящей теории, не только разъясняют принцип биметаллизма, они могли бы послужить средством для учета результатов практического применения этой системы. Если произвольные и недоопределенные функции или кривые, использованные выше, целиком или частично заменить благодаря статистическим данным функциями или кривыми с конкретными коэффициентами, то можно будет приблизительно рассчитать действительные последствия, которые может иметь чеканка дополнительного количества серебряных монет на основе того или иного официального соотношения стоимости золотых и серебряных денег. Предположим, что в стране, к которой относится наш рисунок, после достижения равновесия произошло увеличение количества серебра, но власти воспрепятствовали естественным и необходимым последствиям официального соотношения стоимостей золота и серебра, прекратив чеканку серебряных денег. В этом случае количество денежного серебра останется на уровне IM (Рис. 17), его цена по-прежнему будет представлена расстоянием OP, количество товарного серебра будет соответствовать величине P'I', а его цена — расстоянию OP'. Если после этого возобновляется чеканка серебряной монеты, то последствия официального соотношения будут выражаться в наложении отрезков двух линий P'I' и IN и в перемещении общей линии в положение π'v', между точками P и P'. Очевидно, что при этой комбинации чеканка некоторого количества серебряных денег будет иметь следствием демонетизацию некоторого количества золота, а повышение цены товарного серебра с OP' до Oπ будет иметь следствием снижение цены серебряных денег с OP до Oπ', а цены товарного золота и золотых денег — с ωОР до ωОπ'. Если конкретные цифры могли бы еще нагляднее представить связь рассматриваемых явлений, то вот как они выглядели бы применительно к нашей стране и нашему рисунку. В состоянии равновесия, установившегося при официальном соотношении стоимостей ω=10, совокупное количество серебра OA=PM=5 миллиардов полудекаграммов (порций по 5 граммов — Прим.перев.) распадается на PI = 2 миллиарда в товарном серебре и IM=3 миллиарда в серебряных монетах, а совокупное количество золота AB/10=MN/10=433 миллиона полудекаграммов распадается на MK/10=100 миллионов в золотых монетах и KN/10=333 миллиона в товарном золоте. Цена серебра, выраженная в пшенице, составляет 5 фунтов, а цена золота — 50 фунтов за один полудекаграмм. Иначе говоря, пшеница стоит 0.20 франка за фунт (фунт несколько меньше 0.5 кг — Прим.перев.). Поскольку, согласно принимаемой гипотезе, совокупное количество серебра увеличивается на 2 миллиарда, а чеканка серебряных монет приостановлена, то количество товарного серебра увеличится с 2 до 4 миллиардов, вследствие чего цена упадет с 5 до 1.66 фунта пшеницы за один полудекаграмм. Тогда одну единицу (1) товарного серебра можно будет купить за 0.33=1.66/5 единицы денежного серебра. После того как чеканка серебряных монет будет возобновлена, 2 миллиарда 166 миллионов полудекаграммов серебра останутся в товарной форме, 1 миллиард 833 миллиона превратится в деньги и, с другой стороны, 100 миллионов декаграммов золотых монет будут переплавлены в товарное золото. Цена товарного серебра повысится с 1.66 до 4.33 фунтов пшеницы, цена серебряных денег снизится с 5 фунтов до 4.33 фунта, а цена золота как товара и как денег упадет с 50 фунтов до 43.33 фунта пшеницы за один полудекаграмм. Иначе говоря, пшеница будет стоить теперь 1 франк/4.33=0.23 франка за фунт. Как видим, произошло бы повышение цен всех товаров на 15%.

Примечания

* Альфред Маршалл в статье On Remedies for Fluctuations in Prices, опубликованной в Contemporary Review в марте 1887, описал денежную систему, которая есть не что иное, как биметаллизм с постоянным соотношением количеств.

** При биметаллизме с постоянным соотношением количеств 6-е уравнение должно быть записано как Q''_a=aQ''_o , и математическая теория системы будет состоять в разрешении шести уравнений точно так же, как и в случае биметаллизма с постоянным соотношением стоимостей.

*** Мнение, высказанное Леруа,Болье (Journal des Economistes, январь 1874, p.124).

**** Мнение, высказанное Гернуччи (Journal des Economistes, декабрь 1876, p.457).