В Любом портфеле все отдельные опционы в большей или меньшей степени ведут себя согласно стандартной модели Блэка-Шоулза. Каждый компонент в разной степени вносит свою лепту во всеобщую экспозицию портфеля по акции: положительную или отрицательную. Каждый компонент имеет различающуюся степень временного распада и различную чувствительность к рыночной волатильности. Управляющий таким портфелем должен следить за всеобщим влиянием разных компонентов и ему должна быть доступна оценка воздействия движений цен акций, влияния времени и изменения в волатильности. В этой главе мы покажем, каким образом можно оперировать более сложными опционными портфелями с использованием табличных процессоров. Однако некоторые из обычных опционных стратегий, включающие в себя простые комбинации, могут исследоваться с помощью несложных графических методов, и прежде чем мы рассмотрим более сложные варианты, обратимся к трем простым комбинациям.
7.1 Комбинация №1: вертикальный колл спрэд
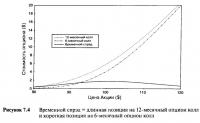
Возможно, самой простой опционной стратегией является вертикальный колл спрэд (иногда определяемый просто как колл спрэд). Эта стратегия включает в себя покупку одного опциона колл и одновременную продажу другого опциона колл с той же самой датой истечения срока, но с иной ценой исполнения. Пример, который мы собираемся рассмотреть, включает в себя $100/$ 110 одногодичный колл спрэд на акцию, о которой мы говорили на протяжении всей книги. Скажем, мы покупаем опцион с ценой страйк $100 и продаем опцион с ценой страйк $110. Если покупать по более низкой цене страйк и продавать по более высокой цене страйк (опционы колл), то согласно рыночной терминологии это будет называться покупкой спрэда. Очевидно, что опцион с более низкой ценой страйк всегда намного дороже опциона с более высокой ценой страйк, поэтому комбинация имеет положительную цену, то есть здесь требуется некоторое инвестирование. Оставляя в стороне вопрос о первоначальной стоимости колл спрэда, рассмотрим стоимость комбинации к моменту истечения срока. Таблица 7.1 и Рисунок 7.1 показывают стоимости к сроку истечения и цены отдельных компонентов, а также итоговый спрэд. Мы используем обычное обозначение, применяемое для коротких опционных позиций, а именно: в виде отрицательной стоимости. Отрицательная стоимость определяет сумму денег, требуемых для ликвидации позиции.
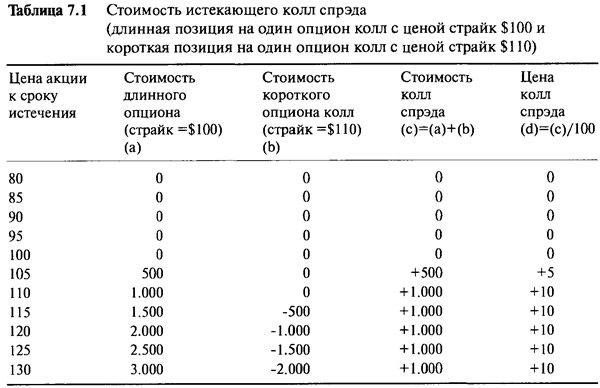
При цене акции ниже $100 оба опциона истекают обесценеными, поэтому спрэд также истекает обесцененым. При цене акции свыше $100, но ниже $110 длинный опцион колл создает экспозицию в 100 длинных акций, но короткий опцион колл дает нулевую экспозицию. При цене акции выше $110 опцион колл с более высокой ценой страйк имеет экспозицию 100 коротких акций, что полностью нейтрализует длинную экспозицию, генерируемую опционом колл с более низкой ценой страйк. Итак, при любой цене свыше $ 110 стоимость колл спрэда ограничена $1.000, а цена колл спрэда будет ограничена уровнем $10 за акцию. Цена к истечению срока, или профиль стоимости ниже $110, очень похожа на цену простой длинной позиции на опцион колл. Добавление короткой позиции на опцион колл устраняет всю дальнейшую прибыль выше уровня $110, закрывая возможность получения неограниченный потенциальный доход от длинной позиции.
Интересно рассмотреть спрэд как единый составной инвестиционный механизм. До этой стадии все рассмотренные нами финансовые инструменты имели прерывность, или изгиб цены при наступлении срока истечения. Рассматриваемый как сложный объект, колл спрэд отличается тем, что имеет два изгиба (two kinks), и это делает линию цены к сроку истечения вдвойне интересной для изучения. Цена колл спрэда к моменту истечения опционов может быть получена из цен двух отдельных компонентов. Таблица 7.2 и Рисунок 7.2 приводят цены отдельных компонентов и спрэда при различных ценах акции со сроком в один год до истечения.
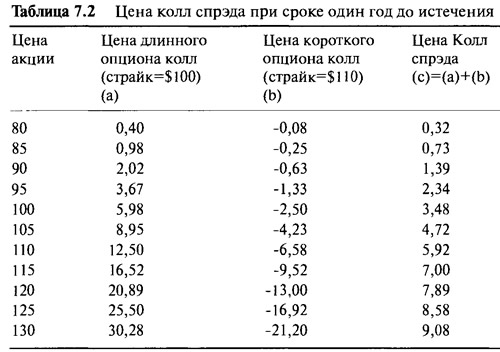
Колл спрэды очень распространены среди решительных инвесторов и спекулянтов, потому что они дешевле, чем просто опционы колл, и требуют меньше движений цены акции для достижения уровня безубыточности. Если инвестор предполагает, что цена лежащей в основе акции значительно поднимется в будущем, то он просто откроет длинную позицию на опцион колл с ценой страйк $100. Однако если он полагает, что цена не поднимется так высоко, а скажем, вырастет только на 10%, то разумнее приобрести колл спрэд. Колл спрэд дешевле просто опциона колл, и если окончательная цена акции незначительно выше $ 110, то завершающие стоимости портфелей будут сходны. Так как спрэд дешевле, то торговый оборот в процентах выше, а спекулянтов обычно очень беспокоит процентный оборот. К примеру, если цена акции равна $100, то опцион колл с ценой страйк $100 стоит $5,98, а спрэд стоит всего $3,48. Если цена акции поднимается до $110 к сроку истечения, то опцион колл будет стоить $10, образуя прибыль в 67%, в то время как колл спрэд, стоимостью те же самые $10, дает прибыль в 187%. Для достижения уровня безубыточности с опционом колл цена базовой акции к истечению срока должна подняться, по крайней мере, до $105,98, в то время как для спрэда подъем до $103,48 будет достаточен. Покупка колл спрэда сопровождается меньшим риском, чем покупка опциона колл, но это компенсируется ограниченным потенциалом роста стоимости.
График цены колл спрэда к наступлению срока истечения представляет собой кривую. На нижних ценовых уровнях акции кривая цены расположена над линией срока истечения, а на высоких уровнях кривая располагается под границей срока истечения. При сроке истечения в один год, наклон профиля цены очень небольшой, и в этой ситуации никогда не бывает больше 0,20. Более подробное исследование чувствительностей колл спрэда можно провести при рассмотрении профиля цены на разных временных уровнях до срока истечения, как это показано на Рисунке 7.3.
Две прерывности, возникающие к сроку истечения, являются причиной того, что колл спрэд имеет очень необычные черты, самая интересная из которых — это влияние временного распада. До настоящего момента мы говорили о портфелях либо страдающих, либо выигрывающих благодаря временному распаду. Этот составной инструмент имеет воздействие и от того, и от другого эффекта. На Рисунке 7.3 хорошо видно, что ниже определенной цены акции ($104 в данном случае) течение времени сокращает стоимость инструмента, но выше определенной цены временной поток увеличивает стоимость инструмента. При определенной цене инструмент абсолютно независим от времени. Поначалу такое поведение кажется очень странным. Когда вы покупаете единственный пут- или колл-опцион, то сразу же после приобретения опциона время начинает разрушать его стоимость. Когда вы продаете единственный опцион, то сразу же после его продажи, время начинает работать на вас. С этим инструментом результат зависит от цены основного инструмента. Причину такого поведения, конечно же, понять несложно — оно такое потому, что портфель одновременно состоит из длинной и короткой позиций на опционы с различными ценами исполнения. Результирующим влиянием временного распада является сумма воздействий временного распада на отдельные компоненты. При ценах ниже $104 отрицательное влияние временного распада более низко расположенного опциона колл перевешивает положительное воздействие временного распада размещенного более высоко (в части цен страйк) опциона колл. При высоких ценах базового актива возникает обратная ситуация, но при определенной цене эти влияния выравниваются.
Как и в случае с отдельными опционами, течение времени приводит к искривлению цены по направлению к границе срока истечения, и изучение траектории кривой может пролить свет на другие виды чувствительности опциона. В данном случае кривая к сроку истечения более сложная и сочетает в себе три линии, соответственно определяющих характер чувствительности. Для краткости рассмотрим две области: над и под определенной ценой акции в $104.
Область нижерасположенных значений
Линии цены в низкой области похожи на профиль цены длинного опциона колл. Вдоль каждой данной кривой значения дельты являются положительными и увеличиваются по мере роста цены акции. С течением времени значение дельты уменьшается при низких ценах и увеличивается при высоких ценах. Изгиб цены, или гамма, является положительной величиной и возрастает по мере приближения к сроку истечения.
Область вышерасположенных значений
Профиль цены в вышележащей области похож на линию цены короткого опциона пут. Вдоль каждой кривой величина дельты уменьшается по мере увеличения цены акции. Истечение времени жизни опциона сказывается аналогичным образом, а именно: увеличивает дельту при низких ценах и уменьшает дельту при высоких ценах. Изгиб цены отрицательный и становится все более ярко выраженным по мере приближения к сроку истечения.
Дельта комбинации всегда положительная или нулевая, поэтому подходящим хеджированием будет являться короткая позиция по базовому инструменту. Первоначально максимальная дельта равна только 0,2 и следовательно, объем хеджа будет довольно маленьким. Это потому, что на большом удалении от срока истечения две противоположные экспозиции акции почти нейтрализуют друг друга. Однако то, что изгиб является положительным в низкой области и отрицательным в высокой области, усложняет попытку игрока волатильностью оставаться дельта-нейтральным. В низкой области гамма позиции положительная, поэтому рехеджирование повлечет за собой продажу акции на пути вверх и покупку на пути вниз — эта комбинация является длинной волатильной позицией. В высокой области гамма позиции отрицательная, поэтому рехеджирование повлечет за собой покупку акции на пути вверх и продажу на пути вниз — такая комбинация является короткой волатильной позицией. На границе между двумя областями существует точка, в которой изгиб, или гамма, переходит от положительного значения к отрицательному, то есть точка, в которой гамма равна нулю и где не требуется никакого рехеджирования. Она соответствует точке, в которой отсутствует воздействие временного распада. В этой точке портфель ни длинный, ни короткий по волатильности, и если он хеджирован правильным количеством акций, то не является ни длинным, ни коротким.
Будет странным, если кто-то захочет оказаться в вышеописанной позиции. До настоящего момента мы предполагали, что прежде чем войти в рынок, индивидуальный игрок решает открыть ему длинную или короткую волатильную позицию, поэтому вышеуказанная комбинация не подходит ни под один из этих случаев. Однако существуют ситуации, когда игрок может предположить: 1) если рынок поднимается, то волатильность будет падать, 2) если рынок падает, то волатильность будет подниматься. Вышеописанная комбинация полностью подойдет для таких прогнозов. Игрок может автоматически открыть короткую волатильную позицию на пути вверх и длинную волатильную на пути вниз.
Другой ситуацией, делающей эту комбинацию еще привлекательнее, является ситуация, в которой игрок оценивает вышестоящий опцион дороже, чем опцион расположенный ниже. Здесь игрок не рассматривает волатильность или направление рыночной цены, а хочет извлечь прибыль из разницы в стоимости опционов. Для этого он должен открыть короткую позицию на дорогой опцион и купить дешевый. Нетго-комби-нация станет адекватной длинной позиции на основной инструмент и чтобы свести риск на нет, необходимо прибегнуть к подходящему хеджированию. Портфель будет таковым либо до истечения срока, либо до исчезновения ценовой разницы, кажущейся аномальной.
Какова бы ни была причина создания такого портфеля, управление рыночным хеджем и наблюдение за воздействием времени и меняющейся волатильностью отнюдь не простая задача, и в этом смысле это — относительно простая комбинация.
7.2 Комбинация №2: временной спрэд
Это одна из первых стратегий, с которой знакомят тех, кто приступает к изучению опционных рынков. Она проста для понимания, позволяя каждому на интуитивном уровне "прочувствовать" понятие временного распада и, равно как и колл спрэд, сопровождается малым риском. Стратегия работает либо с пут, либо с колл опционами, поэтому для упрощения мы будем иметь дело с опционами колл. Логическое обоснование торговли содержат графики на Рисунке 7.4, иллюстрирующие наибольший временной распад, переживаемый опционами на завершающих стадиях своей жизни. Долгосрочные опционы тоже переживают временной распад, но в меньшей степени, чем краткосрочные опционы. Временной спрэд — это попытка извлечь выгоду из этой особенности, и в своей простейшей форме он представляет собой длинную позицию на долгосрочный опцион и короткую позицию на краткосрочный опцион. Идея заключается в том, что если цена основного инструмента движется не очень быстро, то краткосрочный опцион истекает обесцененым и, хотя долгосрочный опцион теряет некоторую временную стоимость, эти потери не будут такими большими, какими были бы потери краткосрочного опциона.
В качестве примера рассмотрим портфель, состоящий из длинной позиции на 12-месячный опцион колл и короткой позиции на 6-месячный опцион колл с одинаковыми ценами исполнения в $100. Рисунок 7.4 показывает ценовые профили отдельных компонентов и сам временной спрэд. На этом рисунке для простоты объяснения короткий опцион показан с положительным значением цены. Стоимость временного спрэда — это разница между двумя кривыми. Заметьте, первоначально портфель не представляет особенного интереса. Один опцион располагает 12 месяцами до срока истечения, а второй — 6 месяцами, оба оцениваются сходным образом, поэтому нетго-позиция будет крайне нечувствительна к изменениям цены акции и волатильности. Лучшее объяснение логики торговли, а также и то, как изменяется ценовая чувствительность, можно найти на Рисунке 7.5, который показывает временной спрэд кривых цены в разное время в будущем. Кривая, отмеченная "6 месяцев до истечения", относится к тому дню, когда долгосрочный опцион становится 6-месячным опционом, а краткосрочный опцион истекает.
Самое лучшее развитие событий для стратегии временного спрэда — это когда краткосрочный опцион истекает в точности около денег. Таким образом, спрэд, который первоначально имел максимальную цену $1,75, заканчивается оцененным в $4,20. Между началом торговли и истечением срока жизни краткосрочного опциона поведение цены временного спрэда очень сложное. Как и в случае с простым колл спрэдом, причина сложностей в том, что портфель имеет два изгиба цен к сроку истечения. В случае с колл спрэдом два изгиба образуются на разных уровнях цены. В случае с временным спрэдом изгибы образуются на одном уровне цены, но в разных точках во времени. Несмотря на то, что обе кривые постепенно сближаются с одной и той же границей срока истечения, делают они это с различной скоростью. Если цена базового инструмента находится возле цены исполнения, то ценовой профиль ровный, поэтому у портфеля нет дельты, а следовательно, нет и экспозиции по акции. Однако при смещении цены исполнения относительно текущих цен базового инструмента комбинация начинает набирать экспозицию по акции. Если цена акции поднимается, то ценовой профиль спадает, поэтому весь портфель становится коротким. Это может быть хеджировано посредством покупки акций. Если цена акции падает ниже цены исполнения, тогда цена портфеля тоже снижается, что может быть хеджировано продажей акций. При нахождении акции около цены исполнения, временной спрэд в сущности является коротким по волатильности, или гамма-коротким. Как и при любых играх с волатильностью, убытки от рехеджирования нейтрализуются положительным временным распадом. Ситуация становится обратной, если опционы глубоко в деньгах или глубоко без денег. При ценах акции, далеких от цены исполнения, временной спрэд имеет положительную гамму и отрицательный временной распад. А теперь мы рассмотрим более сложную стратегию, включающую в себя три опциона.
7.3 Комбинация №3: краткосрочный пут спрэд с пропорцией один к двум и долгосрочный опцион колл
Эта стратегия не относится к разряду стандартных, а является, скорее, комбинацией двух стратегий и используется для объяснения более сложного портфеля. Этот портфель состоит из короткой позиции на два трехмесячных опциона пут с ценой страйк $95, длинной позиции на один трехмесячный опцион пут с ценой страйк $105 и длинной позиции на один шестимесячный опцион колл с ценой страйк $115. Комбинация имеет три точки нарушения динамики: одна на $95, а другая на $105, обе - во временной точке три месяца, третья же находится на $115, а во времени — через шесть месяцев. Стоимость комбинации является суммой цен отдельных компонентов. Однако эта комбинация немного сложнее из-за того, что отдельные позиции отличаются по своим размерам. Посмотрим, как складывается цена портфеля:
Цена комбинации = -2 х (цена 3-месячного опциона пут (страйк $95)) + 1 х (цена 3-месячного опциона пут (страйк $105)) + 1 х (цена 6-месячного опциона колл (страйк $115))
Это верно для каждой из комбинаций опционов, включающих в себя позиции различной величины. Стоимостью комбинации будет сумма отдельных компонентов, взвешенная по размерам позиций. Рисунок 7.6 отражает цену портфеля в разное время и при разных ценах акции.
При очень высоких и очень низких ценах акции комбинация ведет себя так, как будто она просто состоит из длинной позиции на акции и эксперты опционных стратегий знают об этом и без помощи графиков. Причина кроется в том, что при очень высоких ценах акций влияние опционов пут незначительно, а опционы колл настолько глубоко в деньгах, что ведут себя точно так же, как и базовая акция. При очень низких ценах акции влияние опционов колл незначительно. Отрицательная экспозиция акции, генерируемая длинным опционом пут ($105), аннулируется одним из коротких опционов пут ($95). Нетго-позиция становится просто короткой на один оставшийся опцион пут ($95), что конечно же, то же самое, что и длинная позиция на базовый инструмент. Между двумя экстремумами акции поведение цены является сложным из-за параллельных влияний трех различных компонентов. Около цены акции $95 доминирующим компонентом являются короткие опционы пут. Владелец коротких опционов извлекает выгоду из временного распада, поэтому ценовой профиль постепенно поднимается. Около цен акции $105 и $115 длинные опционы имеют противоположное влияние. Конечно же, шестимесячный опцион будет распадаться с меньшей скоростью, чем трехмесячный опцион пут.
На Рисунке 7.6 видно, где комбинация находится в длинной или короткой позиции по рынку, а где комбинация является длинной или короткой по волатильности. Ниже $95 и выше $105 портфель, в сущности, имеет длинную позицию (в различных степенях) на базовую акцию, а между $95 и $105 портфель имеет короткую позицию (в различных степенях) на базовую акцию. Читатель должен суметь распознать поведение ценового профиля в условиях длинной или короткой волатильности. Линия цены, имеющая увеличивающийся (уменьшающийся) наклон по мере роста цены основного инструмента, является кривой длинной (короткой) волатильности. Этот портфель является длинным по волатильности приблизительно от $100 до $130 и коротким по волатильности от $100 до $85.
7.4 Аддитивность чувствительности
При выявлении ценового профиля вышеописанной комбинации линии цен отдельных компонентов, имеющие значение для определения размеров позиций, были просто сложены друг с другом. Само по себе это утверждение вполне очевидно, но процедура эффективна только потому, что отдельные компоненты зависят от цены акции, лежащей в основе, а не друг от друга. (Для портфеля, содержащего различные акции, такая процедура не является приемлемой.). Понятие аддитивности (additivity) цены может быть применимо к большинству сложных портфелей, состоящих из большого количества разных позиций на опционы пут и колл. Однако когда количество разных позиций превышает число три, вышеуказанный графический метод не дает полного представления о стратегии. В конце концов, придется обратиться к компьютерной программе, которая смогла бы прочертить линию цены более сложных портфелей. В основе программы лежит модель Блэка-Шоулза. Мы делаем предположение о том, что цены модели и ценовая чувствительность в точности отражают то, что происходит на рынке. Для большинства рынков и в подавляющем числе случаев это предположение вполне допустимо.
Вспомните, модель требует введения пяти значений (без учета таких параметров, как дивиденды): (1) цена акции, (2) цена исполнения, (3) время до срока истечения, (4) процентная ставка и (5) волатильность. Для упрощения мы рассмотрим только портфель, содержащий одну определенную акцию и любую комбинацию из пут и колл опционов на эту акцию. Также, ради упрощения мы будем использовать одно значение процентной ставки и одно значение волатильности для всех рассматриваемых опционов. (Мы обратимся позже к более сложным аспектам использования различных значений процентных ставок и волатильности для разных опционов.) Процесс подразумевает введение в модель данных о различных ценах акции и сроков истечения, а также сложение (или вычитание, если это короткая позиция) разных результирующих величин, соответствующих размеру опционных позиций. Таким образом, портфель, состоящий из длинной позиции на один опцион по цене $3,50, короткой позиции на два опциона по цене $1,25 и длинной позиции на три опциона по цене $1,00, оценивается по формуле:
Цена Комбинации = 1 х 3,50 — 2 х 1,25 + 3 х 1,00 = 4,00 (7.1)
Для какого-либо общего портфеля цена будет определяться:
Цена Комбинации = (размер №1) х (цена №1) + (размер №2) х (цена №2) + .... и т.д. (7.2)
Характерная аддитивность цен позиций в том, что они хорошо приспособлены для расчетов, особенно при использовании простых табличных процессоров. Все, что нужно уметь, — это считать цены по модели, но даже и они могут быть легко посчитаны в таблице. Таким образом, можно пересчитать стоимость комбинации для любого количества различных цен акций и сроков истечения и отразить результаты на графике. Приспособленность таблиц для решения подобных задач позволяет новичку экспериментировать с различными значениями волатильности и процентными ставками, чтобы понять, какое воздействие они оказывают на более сложные портфели. Большинство цифр, фигурирующих в этой книге, взято из данной программы.
Выделение ценового профиля из комбинации очень полезно и по мере накопления опыта большинство игроков волатильностью будут иметь вполне реальное представление об этом даже без применения программы. Что, пожалуй, самое важное, так это способность точно выявлять линии различных показателей чувствительности. Владелец опциона может пожелать точно знать, насколько длинна или коротка его позиция. Если он находится в длинной позиции по волатильности, ему захочется узнать, когда подойдет момент рехеджирования или значение гаммы своего портфеля. Если он находится в короткой позиции по волатильности, ему нужно знать, сколько денег приносит каждый день временного распада (тэта) и какие возможные убытки он понесет вследствие рехеджирования. Также ему надо знать, как все эти факторы изменятся, если цена основного инструмента завтра или на следующей неделе станет другой, либо если волатильность рынка внезапно увеличится. Короче говоря, владельцу нужно знать не только цену портфеля, но и все показатели чувствительности портфеля к изменениям цены акции, времени и волатильности.
Проблема не так трудна, как кажется на первый взгляд, опять-таки благодаря системе упрощения, предложенной аддитивностью цен. Отдельные значения чувствительности опциона являются скоростью изменения цен, а так как цена комбинации является суммой цен составляющих ее компонентов, то чувствительностью комбинации опционов будет сумма отдельных чувствительностей. Итак, в уравнении (7.1) дельты опционов, соответственно, равняются: 0,40, 0,30 и 0,1, а дельтой комбинации является:
Дельта Комбинации = 1 х 0,40 — 2 х 0,30 + 3 х 0,1 = +0,1 (7.3)
Портфель имеет дельту 0,1, поэтому будет вести себя подобно портфелю, содержащему длинную позицию на 0,1 х 100 = 10 акций. Для какого-либо определенного портфеля дельта выявляется так:
Дельта Комбинации = (размер №1) х (дельта №1) + (размер №2) х (дельта №2) + ... и т.д. (7.4)
Это понятие может быть применимо ко всем чувствительностям, таким, как гамма, тэта и вега, и означает, что расчет риска всего портфеля является ничуть не более сложным, чем простое математическое суммирование (summation).
7.5 Наблюдение за риском сложных опционных портфелей
Изучение ценовых профилей, таких как на Рисунках 7.1-7.6, полезно для получения общего представления о том, как стоимость портфеля изменяется вместе с ценой акции и во времени. Однако, как правило, необходима более детальная классификация всех рисков, которым подвержен портфель, и эти риски должны быть выражены в долларовом значении. Для объяснения одного из способов, с помощью которого можно исследовать риски, вернемся к вышеприведенной комбинации №3. Для того чтобы придать числам больше значимости, помножим все размеры позиций на 100. Рассматриваемый портфель, таким образом, содержит короткую позицию на 200 трехмесячных опционов пут с ценой страйк $95, длинную позицию на 100 трехмесячных опционов пут с ценой страйк $105 и длинную позицию на 100 шестимесячных опционов колл с ценой страйк $ 115. Для упрощения предположим, что все опционы были куплены или проданы по надлежащей справедливой стоимости с использованием 15% волатильности, когда цена акции составляла $100, а процентные ставки равны нулю. Первоначально важно определить три параметра сдвига: сдвиг в волатильности, сдвиг во времени и сдвиг в цене акции. Эти параметры позволяют устанавливать риск, колеблющийся в связи с их изменениями, что выглядит как результат воздействия релевантных переменных.
Сдвиг в волатильности
Основным источником рисков для опционного портфеля является изменение всеобщей рыночной величины волатильности. В рассматриваемом примере мы предполагаем, что портфель создан, когда опционы торговались по ценам, сложившимся при 15% волатильности. А что если волатильность внезапно увеличивается на определенное значение, скажем, на 1% до 16%? Данное значение является сдвигом в волатильности, используемым для определения риска по волатильности (или вега), и в оставшейся части книги мы сделаем это значение равным 1%, хотя можно использовать и другую величину. Колонки с заглавием (+ вол) относятся к изменениям, возникшим в результате увеличения волатильности на 1 %.
Сдвиг во времени
Параметр сдвига во времени в приведенном примере установлен как 1 день (1/365-я года), но конечно же, его значение может быть установлено и для большего периода времени. Это означает, что при чтении таблицы рисков, колонки с заглавием (+ время) должны рассматриваться как изменения, возникшие в результате истечения одного дня.
Сдвиг в цене акции
Будь то длинная или короткая волатильность, управляющий портфелем должен иметь представление о том, насколько быстро меняется дельта портфеля относительно изменений цены основного инструмента, а именно — о гамме позиции. Чем пользоваться текущей скоростью изменения, лучше иметь такой критерий, который определяет различие в позиции по дельте, когда основной инструмент передвигается на определенное значение, то есть сдвиг в цене акции. В этом примере мы устанавливаем сдвиг в цене акции на очень маленькое значение, равное $0,10.
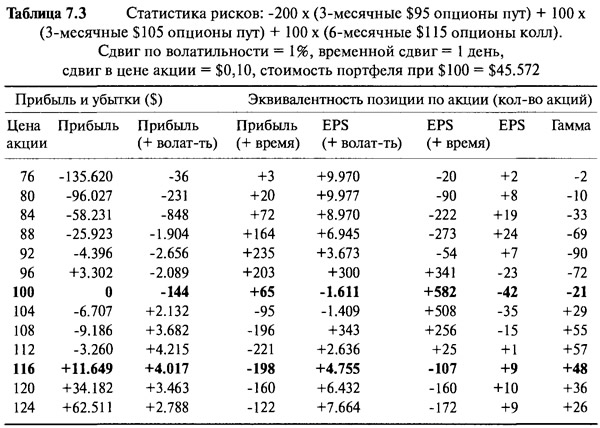
Двумя основными интересующими нас вопросами являются: (1) как изменяется стоимость портфеля и (2) как изменяется экспозиция портфеля по акции? Таблица 7.3 представляет классификацию рисков для рассматриваемого портфеля и разделена на два раздела. Раздел слева отражает прибыль и убытки в долларах, а раздел справа содержит информацию относительно общей рыночной экспозиции по акции. Вначале мы рассмотрим элементы ряда, соответствующего цене акции $100.
- Прибыль и убытки = 0. Общая стоимость портфеля при $100 составляет $45.572. Портфель был создан при цене акции $100, цены не изменились. Следовательно, чистая прибыль на этом уровне равна нулю.
- Прибыль и убытки (+ волатильность) = — $144. Число — $144 отражает изменение всего портфеля, если волатильность увеличилась на значение, определяемое параметром сдвига в волатильности. Поэтому, при прочих равных условиях, если все волатильности увеличиваются на 1%, портфель падает в стоимости на $144. Подобным же образом, при прочих равных условиях, если все волатильности уменьшаются на 1%, то портфель увеличится на $144.
- Прибыль и убытки (+ время) = + $65. Изменение стоимости портфеля, вызванное истечением одного дня. Поэтому при прочих равных условиях портфель увеличивается в стоимости на $65 к следующему дню.
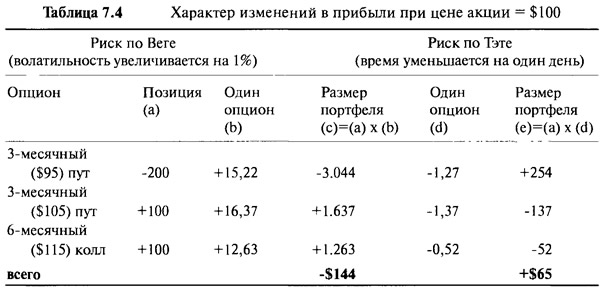
Эти суммы небольшие по сравнению с общей стоимостью портфеля, потому что при такой цене акции положительные и отрицательные влияния изменений волатильности и временного распада на цены отдельных компонентов почти полностью уравновешиваются. Классификация влияний этих изменений по отдельным компонентам представлена в Таблице 7.4.
- ESP = —1.611 акций. Эквивалентность позиции по акции отражает позицию по ее чистой экспозиции. При $100 она равна —1.611, поэтому позиция в состоянии, как если бы портфель имел короткую позицию на 1.611 акций. Игрок волатильностью, не желающий зависеть от направления движения основного инструмента, мог бы ликвидировать риск, купив 1.611 акций.
- ESP (+ волатильность) = +582 акций. Это говорит об изменении в экспозиции по акции, вызванное общим ростом волатильности. При прочих равных условиях, если волатильность увеличивается на 1%, то экспозиция возрастает на 582 акции, поэтому результирующая экспозиция будет равна = -1.611 + 582 = —1.029 акций. Если волатильность уменьшается на 1%, то экспозиция снижается на 582 акции, вследствие чего экспозиция становится = —1.611 — 582 = —2.193 акций.
- ESP (+ время) = — 42 акции. Это означает изменение в экспозиции во времени. На этом ценовом уровне акции экспозиция портфеля уменьшится на 42 акции до — 1.611 — 42 = —1.653 акций к следующему дню.
- Гамма = — 21 акция. Это означает уровень активности рехеджирования, необходимого для поддержания дельта-нейтральности, или скорость, с которой экспозиция акции изменяется. При цене акции около $100 портфель потребует регулирования в размере 21 акции за движение на $0,10. Знак "минус" показывает, что на этом уровне портфель является коротким по волатильности, поэтому небольшие увеличения (уменьшения) цены акции потребуют покупку (продажу) 21 акции на каждом движении в $0,10.
Подводя итог, отметим, что на уровне $100 портфель будет терпеть небольшой убыток, если волатильность увеличится, а его стоимость будет повышаться с течением времени. На уровне $100 позиция становится немного шорт по рынку и немного шорт по волатильности. Теперь рассмотрим влияния на тот же портфель в ситуации (немного нереальной), когда цена акции внезапно поднимается до $116.
- Прибыль и убытки = + 11.649. Портфель увеличился в стоимости на $11.649.
- Прибыль и убытки (+ волатильность) = +$4.017. Это говорит о том, что если волатильность увеличивается на 1%, то возникает дополнительная прибыль в $4.017, поэтому итоговая прибыль благодаря ценовому движению и плюс изменению волатильности будет составлять 11.649 + 4.017 = $15.666. Однако, если волатильность падает на 1%, то прибыль уменьшается на 4.017 = до $7.632. Если волатильность изменяется больше, чем на 1%, то влияние на итоговую прибыль будет значительным. На этом уровне акции для портфеля риск по параметру вега намного больше, чем на уровне $100.
- Прибыль и убытки (+ время) = -$198. Временной распад на этом уровне цены акции теперь составляет -$198 в день. Эти потери будут вычтены из соответствующей прибыли в $11.649.
- ESP = +4.755 акций. На этом уровне портфель имеет экспозицию лонг 4.755 акций, которая будет увеличиваться по мере роста цены акции. В пределе, при очень высоких ценах акции, эта величина достигнет максимального значения в 10.000, и все это — благодаря длинной позиции на 100 опционов колл.
- ESP (+ волатильность) = -107 акций. При прочих равных условиях, экспозиция уменьшится на 107 акций, если волатильность возрастет на 1%. Поэтому при волатильности 16% чистая экспозиция акции будет 4.755 — 107 = 4.648 акций.
- ESP (+ время) = + 9 акций. Течение времени увеличивает экспозицию акции на 9 акций в день.
- Гамма = + 48 акций. До этого уровня гамма является положительной и равна 48 акциям за движение цены на $0,10. Движение от $100 до $116 станет причиной изменения портфеля: от короткого по волатильности до длинного по волатильности. При $100 отрицательный изгиб 200 коротких опционов пут доминирует в портфеле, в то время как при $116 доминирует влияние положительного изгиба длинного $105 опциона пут и длинного $115 опциона колл.
Программа, создающая таблицы рисков, подобные Таблице 7.3, позволяет управляющему опционным портфелем предсказать с большой долей вероятности, что может произойти с его портфелем при любой цене акции в случае, если изменятся рыночные условия. Более того, она позволяет игроку волатильностью увидеть заранее, как будет изменяться хеджирование в различных ситуациях. В дополнение к определению общих свойств портфеля, иногда полезно рассмотреть более детальным образом вклад каждого отдельного компонента в общий портфель. Так как свойства портфеля являются просто суммой отдельных свойств, то изучение этих категорий представляется несложным. Программа дает сведения об отдельных характеристиках, сведенных в Таблице 7.4, тем самым отражая их вклад в общую вегу и влияние теты на прибыль.
7.6 Регулирование профиля риска опционного портфеля
Предположим, управляющий портфелем позволил вышеописанной позиции развиваться нехеджированной до точки, где цена базовой акции равна $116. На этом уровне он переоценит активы в соответствии с текущей рыночной ценой, а именно: будет иметь нереализованную прибыль $11.649 и портфель с экспозицией лонг 4.755 акций. Допустим, на этом уровне управляющий больше не хочет оставаться в длинной позиции по рынку, а желает применить хеджирование. Что ему следует предпринять? Простейшим ответом будет короткая позиция в объеме 4.755 акций. Таблица 7.5 отражает свойства риска хеджированного портфеля. Сравнивая значения Таблицы 7.5 с нехеджированным портфелем, приведенным в Таблице 7.3, мы видим, что единственное различие наблюдается только в колонках EPS и Прибыль; а все остальные свойства риска те же самые. Короткая позиция на 4.755 акций сокращает экспозицию на 4.755 акций на всех ценовых уровнях, а так как цена не имеет изгиба или гаммы, то чувствительность к волатильности и/или времени не подвергается влиянию. Единственные изменения в части прибыли связаны с добавлением короткой позиции на акции по цене $116. Если цена основного инструмента будет снова падать на протяжении всего пути до $100, то чистая прибыль увеличится на 4.755 х (116-100) = $76.080. Изменение риска, вызванное короткой позицией по акции, лучшим образом отображено графически на Рисунке 7.7. Этот график показывает профиль цены хеджированного и нехеджированного портфелей во время начала торга. При цене $116 нехеджированный портфель имеет наклон в 4.755 акций, а наклон хеджированного портфеля равен нулю. Хеджирование акцией вращает всю линию цены до того момента, пока наклон на $116 не сводится к нулю. Также оно сокращает наклон (то есть, экспозицию) кривой везде на 4.755 акций.
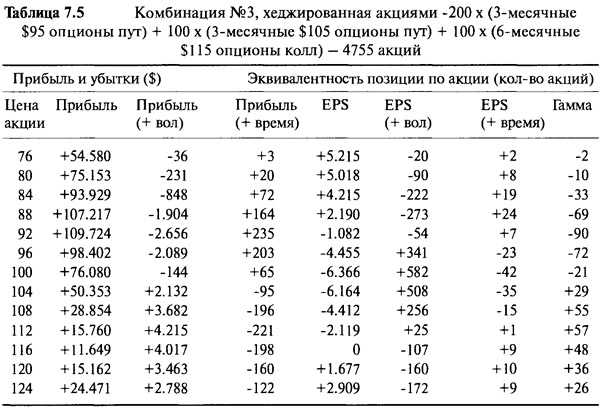
Использование короткой позиции дало желаемый результат ликвидации риска возле уровня $116, но свойства остальных рисков не подверглись влиянию. При $116 портфель является все еще длинным по волатильности и теряет $198 в день. Управляющий может довольствоваться такой ситуацией, а возможно, он захочет ликвидировать некоторый риск временного распада и риск по веге, а также и рыночный риск. Чтобы этого добиться, ему придется рассмотреть вопрос хеджирования не только с помощью акций, но и с использованием опционов. Здесь только один вариант — это короткая позиция на опцион колл, и для упрощения мы остановим свое внимание только на краткосрочных опционах колл с ценами страйк в диапазоне $105 - $125. Таблица 7.6 перечисляет свойства этих инструментов с учетом того, что размер позиции равен 100.
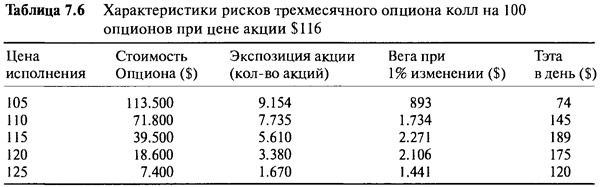
Короткая позиция на любой из этих опционов колл с правильным размером ликвидирует рыночный риск в непосредственной близости от $116 и сократит до некоторой степени риск по веге и тэте. Какой из них управляющий выберет, зависит оттого, какого рода риск он предпочтет. В качестве примера рассмотрим использование опциона колл с ценой страйк $110. Короткая позиция на 100 таких опционов является рыночным эквивалентом для 7.735 коротких акций. Нам нужно открыть короткую позицию только на 4.755 акций, поэтому подходящее количество опционов рассчитывается следующим образом:
Количество коротких колл опционов с ценой страйк $110, необходимое для отрицательной экспозиции 4.755 акций = 100 х 4.755/7.735 = 61
Следовательно, из таких опционов мы продаем в короткую 61 опцион, получая прибыль, равную 61 х (71.800)/100 = $43.798. Также можно посчитать — до того, как мы предпримем это хеджирование — сокращение риска по параметрам вега и тэта. Если 100 опционов имеют вегу $1.734 и тэту $145, то произведя расчеты подобным образом, мы узнаем, что 61 опцион имеет вегу и тэту по $1.058 и $88 соответственно. Итак, короткая позиция на 61 контракт трехмесячного опциона колл с ценой страйк $ 110 имеет двойное действие — ликвидирует рыночный риск в непосредственной близости от $ 116, а также сокращает риск временного распада и риск по веге. Сведения об общем риске этого портфеля представлены в Таблице 7.7, а графическое изображение эффективности использования коротких опционов колл дано на Рисунке 7.8.
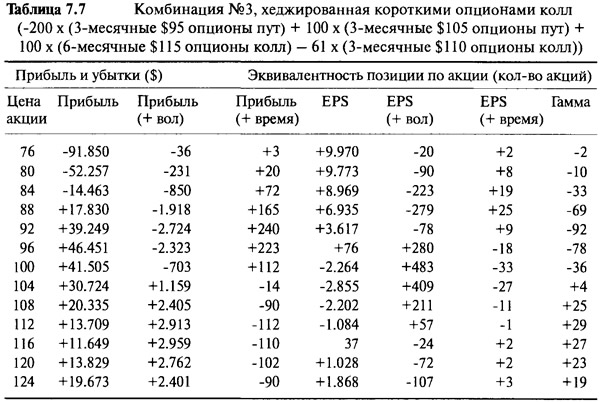
Мы видим, что хеджирование, использующее короткие опционы колл, имеет желаемый эффект в зоне $116. При $116 кривая цены имеет предпочтительный наклон, равный (приблизительно) нулю, и менее выразительный изгиб. Гамма позиции упала с +48 до +27. Заметьте, что при низких ценах акции эффективность падает и все из-за основного свойства профиля короткого опциона колл. Самое большее, что можно заработать при продаже опционов колл, — это взятая при этом премия. При очень низких ценах акции единственной разницей между хеджированной и нехеджированной позицией является премия опциона колл, составляющая $43.798. Это всего лишь один пример использования коротких опционов колл для хеджирования, и читателю остается самому определить, каков будет эффект при использовании других цен исполнения.
Третий способ решения проблемы хеджирования, состоящей в ликвидации экспозиции длинных акций, лежит в покупке опционов пут. Рассмотрим свойства шестимесячного опциона пут, приведенные в Таблице 7.8: 100 опционов пут с ценой страйк $125 дают отрицательную экспозицию в 7.430 акций. Нам нужна короткая позиция только на 4.755 акций, чтобы нейтрализовать комбинацию 3. Таким образом, требуемое количество акций вычисляется следующим образом:
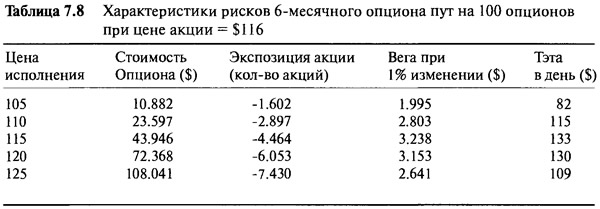
Количество коротких опционов пут с ценой исполнения $125, необходимое для отрицательной экспозиции 4.755 акций = 100 х 4.755/7.430 = 64
Применяя подобные расчеты, можно показать, что 64 длинных опциона пут увеличивают вегу и тэту на $1.690 и $70 соответственно.
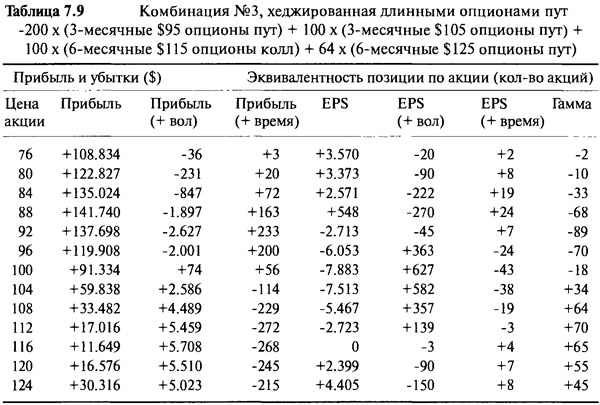
Таблица 7.9 и Рисунок 7.9 отражают свойства хеджированного портфеля. Как и прогнозировалось, вега и тэта увеличились так же, как и гамма. При $116 портфель становится лонг с гаммой 65, что следует из увеличивающегося изгиба. Использование длинных опционов пут имеет полностью обратный эффект по сравнению с использованием коротких опционов колл. При очень низких ценах 64 длинных опциона пут делают взнос на 100% и дают отрицательную экспозицию в 64 х 100 = 6.400 акций. Если цена акции поднимается, то длинные опционы колл с ценой страйк $115 свободно увеличиваются в стоимости, и ни короткие опционы колл, ни короткие акции не влияют на них при пути наверх. Использование опционов пут для хеджирования способно увеличивать рост прибыли, если цена акции поднимается или падает. В нижней части тэта-распад намного больше. Хеджирование длинными опционами пут просто увеличивает степень лонг по волатильности. Рисунок 7.10 демонстрирует три различные стратегии хеджирования. Управляющий выбирает стратегию, основываясь на своем отношении к рыночной волатильности.
7.7 Аппроксимация оценки риска больших ценовых движений
Программа, подобная той, что рекомендуется в книге, очень удобна для точного определения различных типов рисков, связанных со сложными портфелями. Однако существуют технические приемы, которые дают приблизительные расчеты позиции по риску, не требующие применения программ. Управляющие несколькими различными опционными портфелями считают эти методы эффективными для получения быстрого обзора предельных рисков, связанных с большими ценовыми движениями акций. Если портфель состоит из большого количества разных длинных и коротких позиций на пут- и колл-опционы, то можно воспользоваться быстрым методом, игнорирующим влияние временного распада и волатильности, а также основывающегося на предположении, что все опционы будут торговаться по внутренней стоимости. Этот метод имеет силу только около истечения срока и/или при очень низкой волатильности, но дает хорошее представление о рисках, связанных с большими ценовыми движениями. При больших подвижках цен мы можем быть уверены в том, что все опционы будут либо глубоко в деньгах, либо глубоко без денег. Почти при всех обстоятельствах опционы, которые глубоко в деньгах, торгуются по внутренней стоимости и, следовательно, дают максимально возможную экспозицию по акции. А опционы, которые глубоко без денег, обесцениваются и соответственно имеют нулевую экспозицию по акции.
Начиная с опционов колл, процедура осуществляется следующим образом. Если все опционы торгуются по внутренней стоимости, то длинные позиции на опционы колл будут иметь экспозицию +100 акций над ценой страйк и нулевую экспозицию ниже цены страйк. Короткие позиции по опционам колл будут иметь экспозицию -100 акций над ценой страйк и нулевую экспозицию ниже цены страйк. В качестве примера рассмотрим портфель, состоящий из опционов колл. Все его характеристики приведены в таблицах на Рисунке 7.11. Для них используется обычное обозначение: "+" отражает длинную позицию, а " короткую. Обратите внимание на две противоположные экспозиции акции каждого опциона по обе стороны каждой цены страйк.
Начните с опциона, чья цена страйк самая маленькая. Под минимальной ценой страйк рассмотрите все опционы колл, которые имеют нулевую экспозицию. Над первой ценой страйк экспозиция будет равна экспозиции минимального опциона колл (в данном случае, длинная позиция на 300 акций). Идите выше, к следующей цене страйк и прибавьте экспозицию этой позиции к существующей позиции. Итак, на цене исполнения в $95 экспозиция ниже $95 составляет 300 длинных акций, но выше $95 — уже 100 коротких акций. Идите к следующей цене страйк и продолжайте до последнего опциона. Мы видим, что при любой цене выше $110 портфель состоит из 300 коротких акций. Цифры между каждой ценой страйк дают приблизительный расчет вероятной экспозиции, если опционы торгуются по внутренней стоимости. Цифры могут быть использованы и для приблизительного расчета вероятной прибыли и убытков портфеля. Если управляющий создает портфель в то время, когда цена акции составляет $100, тогда движение до $105 при экспозиции +200 акций принесет заработок 200 х 5 = $1.000. Падение в цене до $95 тоже принесет доход (потому что экспозиция по акции ниже $95 отрицательная) 100 х 5 = $500. Прибыль или убытки, связанные с большими ценовыми движениями, могут быть рассчитаны просто путем сложения соответствующих экспозиций, умноженных на интервал цены исполнения.
Процедура с опционами пут обратная. Используем пут-опционный портфель, приведенный на Рисунке 7.11, в качестве примера. Каждая длинная позиция на опцион пут дает экспозицию -100 акций под ценой исполнения и нулевую экспозицию над ценой исполнения. Каждая короткая позиция на опцион пут дает экспозицию +100 акций под ценой исполнения и нулевую экспозицию над ценой исполнения. Умножение размера каждой позиции на соответствующую экспозицию дает значение отдельных вкладов. Для того чтобы узнать общую экспозицию, начните с самой высокой цены страйк. Над максимальной ценой страйк ($110) все пут опционы имеют нулевую экспозицию. Под максимальной ценой страйк экспозиция будет такой же, как и у пут опциона (-300 акций в данном случае). Идите ко второй по величине цене страйк ($105). Позиция здесь короткая — на 3 опциона пут, поэтому добавляется +300 акций ниже $105. Прибавьте экспозицию по акции этого опциона пут к существующей позиции, в результате чего получается нулевая экспозиция. Повторяйте процедуру до самой низкой цены исполнения. В завершение сложите экспозиции пут и колл опционов вместе, сообразуясь с ценой на акцию, и получится значение общего направленного риска комбинации. Этот приведенный нами пример, который мы назовем комбинацией №4, является коротким по рынку выше $ 105 и между $90 и $95, длинным между $95 и $105 и нейтральным ниже $90.
Следует отметить, что такой подход к управлению риском дает только приблизительные результаты. Если оставшееся время до истечения срока больше нескольких недель и подразумеваемые волатильности опционов не являются малыми, то невозможно сделать предположение, что все опционы торгуются по внутренней стоимости. Однако метод позволяет сделать очень хорошие расчеты направленного риска при больших ценовых движениях. Вышеописанный портфель подвержен риску серьезных изменений цен акций.
7.8 Приблизительная оценка риска по волатильности
При определенных обстоятельствах без использования сложных программ можно получить приблизительное представление о том, каким является портфель: коротким по волатильности или длинным по волатильности. Как объяснялось в разделе 6.5, игрок волатильностью оценивает опционы пут и опционы колл одинаково: его интересует только степень положительного или отрицательного изгиба цены. Все, что нужно знать, это содержит портфель длинную или короткую позицию на опционы. Процедура исключения предлагает очень удобный метод, и для объяснения вернемся к комбинации №4. Портфель представлен как нетто-позиция опционов в Таблице 7.10.

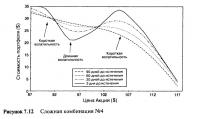
При волатильной торговле больше всего нас интересуют комбинации гаммы при различных ценах акции. Во многих опционных портфелях гаммой всего портфеля является сумма гамм его отдельных частей. Каждое отрицательное влияние нейтрализуется соответствующим положительным влиянием. Каждая короткая опционная позиция вносит отрицательную гамму, а каждая длинная опционная позиция вносит положительную гамму. Конечная гамма при каждой определенной цене акции зависит от важности соответствующих гамм отдельных компонентов. Обратите внимание на Рисунке 4.11, что гамма опциона максимальная (или минимальная, если короткая позиция), когда опцион находится около денег. Абсолютная величина максимальной (минимальной) гаммы также зависит от оставшегося времени до истечения срока. Если опцион имеет в запасе мало времени, скажем один месяц или меньше, то изменения в гамме около денег большое. Если у опциона еще есть время до истечения срока, скажем три месяца или больше, то линия гаммы сравнительно ровная. Это дает возможность относительно легко изучать нетто-позиции опционов. Если опционы около даты срока истечения, то влияние гаммы будет сосредоточено вокруг каждой цены страйк, а если дата истечения срока еще далеко, то влияние гаммы будет более рассеянным и не будет сосредоточено на определенных ценах исполнения. Значительная опционная позиция в комбинации №4 имеет характер короткой при ценах страйк $95 и $105 и длинной с ценой страйк $95. При трех месяцах до истечения срока влияния гамм отдельных опционов настолько малы и похожи, что можно сделать допущение, что все они одинаковы, таким образом, рассматривая портфель как состоящий только из конечных опционных нетто-позиций, т.е. = —3. За три месяца, или более до истечения срока общий портфель имеет просто короткую позицию на 3 опциона и малую степень отрицательного изгиба. Эти утверждения подкреплены графиками цен на Рисунке 7.12.
7.9 Торговля волатильностью и манипулирование рынком
Время от времени торговцев волатильностью обвиняют в образовании аномальных ценовых движений акций или даже в манипулировании рынком. Чтобы понять, в чем состоит смысл манипулирования рынком, рассмотрим ситуацию с двумя торговцами: один из них — торговец длинной волатильностью, другой — короткой волатильностью. Для простоты объяснения давайте предположим, что соответствующие портфели содержат только один опцион: колл опцион на акцию с ценой страйк $100, который хеджирован акцией. Давайте сначала рассмотрим ситуацию с игроком длинной волатильностью. У него длинная позиция на опцион колл и короткая позиция по основному инструменту. Он надеется на то, что от начала торга до наступления срока истечения цена базовой акции будет сильно колебаться. Если колебания будут возникать вокруг цены исполнения, то прибыль будет еще больше. При цене акции, почти равной цене исполнения, гамма будет максимальной, требующей огромного количества сделок по рехеджированию, каждая из которых будет фиксировать прибыль. Теперь рассмотрим ситуацию, в которой дата истечения срока совсем близко: скажем, она наступит через неделю или через день. Опционы переживают наибольший временной распад на последних стадиях своей жизни, в особенности если цена акции приближается к цене исполнения. При этом всегда возникает опасность того, что если опцион на последней стадии все еще около денег, то волатильность может совсем исчезнуть. Худшим вариантом для игрока длинной волатильностью является истечение опциона около денег (см. Рисунок 4.16). Игрока интересует прежде всего то, чтобы опцион истекал либо в деньгах, либо без денег, особенно если движение окончательной цены неожиданно.
Чтобы увидеть, какая прибыль может быть заработана на последних стадиях жизни опциона, рассмотрим ситуацию, в которой при одном дне до срока истечения цена акции равна $99,9, а портфель имеет длинную позицию на 100 опционов. При этой цене и подразумеваемой волатильности в 15% опцион оценивается по $0,27, имея дельту 0,45. Опцион хеджируется 0,45 х 100 х 100 = 4.500 акциями шорт. Опцион будет стоить 0,27 х 100 х 100 = $2.700, и эта сумма будет потеряна, если цена акции будет равна $100 или ниже при наступлении срока истечения. Если же до наступления срока истечения цена акции внезапно продвинется либо вверх, либо вниз, а хеджирующая позиция останется неизменной, то в итоге получится приличная прибыль. Таблица 7.11 показывает прибыль в случае двух разных ценовых движений.

Итак, владелец этого портфеля будет очень доволен, если цена акции внезапно начнет двигаться в сторону от цены исполнения прямо перед наступлением срока истечения. Некоторые игроки знают, как заставить цену акции двигаться. Поэтому вместо того, чтобы надеяться на случай, они вводят огромное количество ордеров на покупку или продажу прямо перед наступлением срока истечения. В некоторых случаях рынку совсем не обязателен сильный толчок, если учитывать, что для каждой длинной позиции существует короткая позиция. Когда один участник сделки, имея короткий по волатильности портфель, толкает цену акции в какую-либо сторону, может возникнуть цепная реакция. Для поддержания дельта-нейтральности владелец короткой позиции по волатильности должен продавать акции, если цена падает. В вышеприведенном примере, если цена акции продвинулась от $99,9 до $99,5, то игрок короткой волатильностью может дать сигнал к продаже. Дальнейшая продажа может вызвать эскалацию продаж, в результате чего к наступлению срока истечения цена может значительно упасть. И все это может начаться с инициативы игрока длинной волатильностью, который ввел сравнительно небольшой ордер на продажу.
Стратегию манипулирования рынком отличает то, что игроку длинной волатильностью, по определению, следует покупать, когда цена основного инструмента падает, и продавать при ее росте. Но чтобы опустить цену акции, он должен продавать на падающем рынке, а чтобы поднять цену, он должен покупать в поднимающемся рынке — стратегия абсолютно противоположная его торговым правилам. Итак, если игрок длинной волатильностью решает манипулировать рынком, он должен быть уверен в том, что расходы, связанные с манипуляциями, не превысят ожидаемую прибыль.
Теперь рассмотрим игрока короткой волатильностью. Лучшим вариантом для него будет, если опцион заканчивается в точности около денег (см. Рисунок 5.6). На последних стадиях жизни опциона ему выгоднее всего манипулировать ценой акции таким образом, чтобы она оказалась как можно ближе к цене исполнения. Если цена акции начинает падать на большой отрезок от цены исполнения, тогда возникнет необходимость покупки для поддержания рынка, а возможно, и возврата цены акции обратно вверх, к цене исполнения. Если цена акции начинает значительно подниматься от цены страйк, тогда игроку лучше всего будет продать акцию для того, чтобы остановить подъем и, вполне возможно, вынудить цену опуститься назад, вниз. Но для того, чтобы оставаться дельта-нейтральным, игроку короткой волатильностью следует продавать на пути вниз и покупать на пути вверх. Если игрок решает манипулировать рынком, то он, точно так же, как и игрок длинной волатильностью, вынужден нарушать правила, которые сохраняют его дельта-нейтральность, и тем самым подвергает себя направленному риску. Манипулирование рынком может привести к потере огромной суммы денег.
Совершенно очевидно, что на некоторых рынках окончание торговли опционной серии совпадает с необычными ценовыми движениями. На рынках опционов, торгуемых на американские индексы, определенные дни срока истечения, когда одновременно завершают жизнь опционы разных рынков, считаются днями тройного колдовства1. В начале 90-х годов крупные игроки, участвовавшие на рынке опционов, торгуемых на индекс Никкей-225 в Осаке, спровоцировали движение до 5% за ночь. Часто две противоположные стороны инвестирования занимают позиции огромного размера на опционы лишь за 12 часов до наступления срока истечения и вводят огромное количество ордеров на покупку или продажу на рынке базовых ценных бумаг. При наступлении срока истечения одна сторона зарабатывает 20 миллионов долларов за счет другой стороны, а при следующем истечении срока, эта же сторона теряет 20 миллионов. Для мелких рыночных игроков это подобно столкновению титанов.
Возможно, самый известный пример манипуляции рынком — разорение старейшего коммерческого банка Англии — "Барингс- банка"2. К февралю 1995 года трейдер Барингс-банка на рынке фьючерсов и опционов, которые обращаются на индекс Никкей-225 в Сингапуре (рынок SIMEX) открыл огромное количество коротких опционных позиций на индекс. Эти опционы исполнялись через фьючерсные контракты на индекс. (Не будем здесь подробно говорить о самих фьючерсных контрактах, просто отметим, что длинный фьючерсный контракт имеет тот же самый риск, что и длинная позиция на лежащую в основе индекса корзину акций. Если кто-то имеет длинную позицию по фьючерсному контракту, а рынок падает, то он несет убытки). Трейдер имел гигантскую короткую позицию по волатильности — возможно, самую большую короткую позицию по волатильности из тех, которые когда-либо открывались. Предшествующий этому событию год был одним из наиболее стабильных. Индекс Никкей-225 торговался в очень узком диапазоне + или — 5% на протяжении более шести месяцев, и трейдер был уверен, что так оно и будет продолжаться. Но 25 февраля в Японии произошло землетрясение.
Руководители фондов, оперирующих ценными бумагами, недоумевали по поводу того, что рынок фьючерсов на индекс Никкей-225 незамедлительно вслед за этим не упал. Землетрясение предполагало возникновение серьезных предпосылок для переоценки рынка ценных бумаг, и большинство участников рынка ожидали падение, по крайней мере, на 5%. Многие начали активно продавать фьючерсы в ожидании краха рынка и были потрясены легкостью исполнения ордеров: создавалось такое впечатление, что где-то находится таинственный покупатель, покупатель "крупного калибра". Трейдер Барингс-банка находился в крупной короткой позиции по волатильности и, если бы рынок падал, то ему пришлось бы продать бесчисленное количество фьючерсных контрактов для поддержания дельта-нейтральности. Он осознавал, что требуемое рехеджирование может быть столь огромным, что подтолкнет рынок к еще большему краху, чем ожидалось после землетрясения, поэтому он решил попробовать манипулировать всем японским рынком ценных бумаг: он покупал фьючерсы вместо того, чтобы их продавать. Именно благодаря этому рынок сразу и не упал. Трейдер Барингс-банка покупал, вопреки огромному давлению со стороны продавцов со всего мира. Это продолжалось несколько дней. За следующую неделю трейдер Барингса собрал десятки тысяч длинных фьючерсных контрактов, в попытке поддержать рынок. В конце концов, у него не осталось денег, и, по его собственным словам, он "больше не мог поддерживать рынок". Когда его действия получили огласку, весь остальной рынок узнал, что Банк Англии (от имени Ба-рингс, который стал банкротом) будет "паникующим" продавцом, и сразу же упал на 1000 пунктов. На тот день убытки составили 860 миллионов фунтов стерлингов, в результате чего один из самых уважаемых банков мира потерпел фиаско. А все из-за того, что короткая волатильная сделка уплыла из-под его контроля. Можно манипулировать какой-либо акцией, но пытаться держать в руках второй по величине в мире рынок ценных бумаг, действуя против естественных сил, было слишком амбициозно.
Последний вопрос, который стоит затронуть, упоминая о банкротстве Барингса, - это вопрос убытков. Средства массовой информации в то время не переставали выдавать сенсации, публикуя новые данные о размерах потерь, которые, несомненно, были огромны. Но никто ничего не сказал о прибыли. Игра на фьючерсах и опционах - игра с суммой, равной нулю. На каждый потерянный доллар существует один заработанный доллар. Если Барингс потерял 860 миллионов фунтов стерлингов, то это значит, что кто-то их заработал, но, похоже, никто не стал даже и задаваться этим вопросом. Барингс был в короткой позиции по волатильности, играя против всех, кто находился в длинной позиции по волатильности, и они спокойно положили свою прибыль в карман. Ни одного цента не было потеряно. Все, что произошло, так это переток 860 миллионов фунтов стерлингов из одних рук в другие.
7.10 Синтетические опционы из динамической торговли акциями
В разделе 6.5 мы объяснили, как можно синтезировать длинную позицию на опцион пут из длинной позиции на опцион колл и короткой позиции по акции. Также мы показали и то, как можно синтезировать колл позицию из пут позиции и акции, и говорили, что на самом деле, все что нужно для создания третьего инструмента, — это располагать двумя инструментами. Синтез одного инструмента из двух других, в сущности, является трансформацией прерывности при истечении срока из одной формы в другую. А если нет зарегистрированных пут- или колл-опционов на интересующую нас акцию? Если у нас нет инструмента с прерывностью цены, с чего нам начать? Сейчас мы докажем, что совсем не обязательно располагать опционами, торгуемыми на рынке, — можно синтезировать опционную позицию, просто динамично торгуя акцией.
Для того чтобы понять, как это делается, рассмотрим поведение трех менеджеров фондов "А", "В" и "С". Менеджеры "А" и "В" совместно управляют дельта-нейтральным коротким по волатильности портфелем, а менеджер "С" управляет спекулятивным фондом. Всех троих интересует определенная акция, которая в настоящее время торгуется по $99 и имеет одногодичный опцион колл с ценой исполнения $100, который торгуется при подразумеваемой волатильности 15%, то есть по цене $5,46. Дельта опциона равна 0,50, поэтому хеджированный портфель первоначально состоит из одного короткого опциона колл и 50 длинных акций — исходная установка, описанная в пятой главе.
"А" и "В" ответственны за два разных элемента короткого по волатильности портфеля. "А" следит за ценой короткого опциона колл и больше ничего. "В" отвечает за рехеджирование, покупая при повышении цены и продавая при падении цены. Давайте представим, что "А" и "В" ведут отдельные записи прибылей. "С" надеется, что цена акции поднимется к концу года, поэтому сразу же покупает один опцион колл. Рассмотрим два разных варианта.
Падение цены акции
Если цена падает к окончанию года, то опционы истекают обесцененными. Менеджер "Л', у которого короткая позиция на опцион, заработает прибыль. Падающая цена означает, что хеджирование длинными акциями принесет убыток. Как только цена упадет, акция продастся с (маленькими) дополнительными потерями. В конце года менеджер "В" останется в убытке. "С" также будет в убытке.
Подъем цены акции
Если к окончанию года цена акции значительно поднялась, то опционы становятся в деньгах, и менеджер "Л' внесет у себя строку об убытках. При поднимающихся ценах менеджер "В" запишет себе прибыль, которая будет увеличиваться по мере добавления акций на пути наверх. "С" также получит прибыль.
Что бы ни случилось, итоговая прибыль всего хеджированного портфеля составит сумму прибылей и убытков руководителей "А" и "В". Если мы предположим, что действительная волатильность цены акции через год составит точно 15%, то хеджированный портфель достигнет уровня безубыточности, какова бы ни была окончательная цена акции. Для достижения уровня безубыточности убытки одной стороны портфеля должны быть в точности равны прибыли другой стороны.
Давайте рассмотрим ситуацию, в которой цена акции движется с волатильностью 15%, но в итоге заканчивает год на уровне $110. Менеджеру "А", который изначально продал опцион по $5,46, придется купить его обратно по $10 и, таким образом, записать убыток 100 х (10 — 5,46) = $454. Весь хеджированный портфель достигнет уровня безубыточности, поэтому менеджер "В" должен записать прибыль $454, которая состоит из всех прибылей от разного количества длинных акций, приобретенных на протяжении жизни опциона. Менеджер "С", который просто купил исходный опцион по цене $5,46 в надежде, что рынок поднимется, запишет прибыль 100 х (10 - 5,46) = $454 — в точности такую же, что и у менеджера "В".
Теперь рассмотрим ситуацию, в которой цена акции движется с волатильностью 15%, но в итоге заканчивает год на уровне $90. Опцион закончится обесцененным. Менеджер "А", который изначально продал опцион по $5,46, запишет, таким образом, прибыль 100 х (5,46 — 0) = $546. Весь хеджированный портфель достигнет уровня безубыточности, поэтому менеджер "В" должен записать убыток в $546, который состоит из всех убытков по разному количеству длинных акций, существовавших на протяжении жизни опциона. Менеджер "С" полностью потеряет свою долю, а именно: 100 х 5,46 = $546 - это точно такой же убыток, что и у менеджера "В".
То, что прибыли и убытки менеджеров "В" и "С" одинаковы, не является совпадением, если смотреть на трех игроков с другой точки зрения. Можно предположить существование прямой связи между "Л' и "С". Менеджер "А" имеет короткую позицию на один опцион, а менеджер "С" имеет длинную позицию на тот же самый опцион. Если бы "А" и "С" совместно управляли фондом, тогда конечным результатом явилось бы то же самое - уровень безубыточности. "А" и "С" имели бы равные и противоположные позиции на один и тот же инструмент, поэтому в итоге фонд был бы полностью нейтральным. Именно этого и пытается добиться менеджер "В". Он старается путем динамического рехеджирования полностью нейтрализовать прибыль или убытки короткой позиции по опциону колл. Менеджер "В" в динамике пытается получить нейтрализующую длинную позицию на опцион колл. Мы можем рассматривать портфель менеджера "В", как в сущности искусственную длинную позицию на опцион колл. Динамическое хеджирование короткого опциона колл в дельта-нейтральном портфеле с высокой степенью точности воспроизводит длинную позицию на опцион колл. И делается это только лишь с помощью акции. Мы видим, что совсем не обязательно наличие торгуемых на бирже опционов - их можно синтезировать путем динамического репродуцирования (dynamic replication).
Здесь необходимо сделать важное добавление. Выше мы предположили, что какова бы ни была окончательная цена акции, имевшая место волатильность всегда была равной 15%. А что если действительная волатильность на протяжении жизни опциона отличалась от 15%? Если действительная волатильность была ниже (выше) 15%, тогда совместно управляемый короткий по волатильности портфель принес бы прибыль (убытки). Скажем, действительная волатильность во время жизни опциона оказалась бы равной только 10%. При 10% первоначальная цена опциона была бы $3,49, то есть на 5,46 — 3,49 = $1,97 ниже цены опциона при волатильности 15%. Эта разница в цене, равная $1,97, или разница в стоимости, равная $197, составила бы итоговую прибыль, совместно полученную менеджерами "А" и "В". Они открыли короткую позицию по волатильности при 15%, а на самом деле она оказалась 10%. В такой ситуации, даже если цена акции заканчивает год на $110, итоговая прибыль портфеля остается равной $197. При $110 менеджер "К все так же теряет 10 - 5,46 = $4,54 за акцию или $454, как и до этого, но зарабатывает чистую прибыль, равную $197. Менеджер "В" должен заработать прибыль, равную 454 + 197 = $651. Роль менеджера "В" абсолютно та же, что и была, а именно: синтез длинной позиции на опцион колл, но на этот раз прибыль оказывается большей, благодаря тому, что волатильность оказалась ниже. Это как если бы менеджер "В" синтезировал опцион колл при более низкой премии соответствущей справедливой стоимости при подразумеваемой волатильности в 10%. Синтез опциона колл по еще более низкой цене привел бы к большей прибыли. В этом и состоит привлекательная сторона синтеза опционов колл путем динамической торговли акцией. Цена, которую вы платите за опцион, является прямой функцией волатильности, сложившейся на протяжении жизни опциона. Она может полностью отличаться от цены, которую вы платите, когда покупаете торгуемый на рынке опционный контракт. Если вы покупаете именно такой опцион, тогда цена, которую вы за него отдаете, является ожидаемой будущей волатильностью (expectedfuture volatility). Когда вы динамично синтезируете опцион, то цена, которую вы платите, является действительной будущей волатильностью (actualfuture volatility).
В последнем примере мы предположили, что реальная волатильность оказалась ниже и составила 10%. Можно следовать той же аргументации в ситуации с волатильностью, оказавшейся выше, скажем равной 20%. При 20% опцион стоил бы $7,44, то есть на $1,98 за акцию больше, чем при 15%. При волатильности, равной 20%, портфель бы потерял 100 х 1,98 = $198, и это произошло бы потому, что какова бы ни была цена акции, стоимость синтеза длинного опциона колл на $198 выше, чем ожидалось.
Приведенный выше пример показывает, как можно синтезировать длинный опцион колл. Начинаем с установления длинной позиции на акцию. Если цена поднимается, то вы покупаете еще акции, а если цена падает, вы продаете акции. В конце намеченного периода прибыль и убытки портфеля с акциями будут равны прибыли и убыткам, которые вы бы имели, если бы просто купили опцион колл. Стоимость искусственного опциона колл не будет известна до конца периода. Если волатильность акции была достаточно низкой, тогда и стоимость опциона будет низкой. Если волатильность была высокой, стоимость окажется тоже высокой.
Понятно, что если инвертировать первоначальные позиции "А", "В" и "С", то несложно будет рассмотреть вопрос получения короткого опциона колл. С помощью того же процесса можно синтезировать длинную или короткую позицию на опцион пут. Синтез опционов пут получил большую популярность в 80-х годах. Этот прием был известен как страхование портфеля (portfolio insurance). Биржевой рынок предлагал к торговле только ограниченное количество опционов на ограниченное количество акций, и индустрия страхования портфелей активно развивалась, имея предложение опционов пут с любой предпочтительной датой истечения срока на любой портфель акций. Одним из действительно важных факторов продажи страхования портфелей был фактор стоимости. На очень спокойных рынках стоимость синтетического воспроизведения была очень низкой. Самыми уникальными были ситуации, когда цена акции оставалась абсолютно неизменной на протяжении всего периода. Короткие опционы пут получаются путем первоначального установления короткой позиции на акции или короткой позиции на фьючерс, торгуемый на индекс. Во всех примерах, рассматриваемых нами в этой книге, мы предполагали, что процентные ставки равны нулю. На практике, конечно же, они всегда больше нуля. При реальной процентной ставке короткая позиция на акцию приносит процентные доходы. Поэтому можно представить себе ситуацию, в которой искусственный опцион пут на акцию на самом деле имеет отрицательную стоимость, — несомненно, чрезвычайно привлекательное предложение. Если цена акции находится в стагнации на протяжении жизни искусственного опциона, тогда не будет никакой торговли, что обусловливает отсутствие торговых убытков. Отсутствие торговых убытков подразумевает, что опцион пут, в конце концов, ничего не будет стоить. Если короткая позиция на акцию приносит доход от процентов, тогда опцион пут фактически вносит свою долю в чистую прибыль, а не создает издержки.
Крах фондового рынка 1987 года обнажил некоторые изъяны концепции страхования портфеля. Динамически синтезированные опционы пут требовали продажи все большего количества акций (или фьючерсов на фондовый индекс) по мере падения цены. Во время краха рынок так стремительно падал, что все больше и больше искусственных опционов пут инициировали все больше и больше ордеров на продажу, вынуждая рынок падать еще ниже. Проблема возникала с исполнением ордеров. Цены двигались настолько быстро, что, в конце концов, торговать стало невозможно. Некоторые участники рынка причину этого краха видели в индустрии страхования портфелей.
Вернемся к стратегии управления сложными портфелями опционов, таких как комбинации № 1 — №4. Если портфель сохраняет свою дельтанейтральность за счет длинной или короткой акции, тогда то, что делает управляющий, является синтезом противоположно направленных опционных портфелей. Простейший из портфелей (комбинация № 1 - вертикальный колл спрэд) имеет длинную позицию на один опцион колл и короткую позицию на один опцион колл. При одних ценах акции изгиб является отрицательным, а при других — положительным. Сохранение такой комбинации в дельта-нейтральном состоянии требует продавать акции на поднимающемся рынке по одним ценам, а на падающем рынке продавать акции по другим ценам. Если кто-то отделяет сделку по акции от остального портфеля, это означает, что он практикует динамическое получение обратного колл спрэда. То же самое подходит и для более сложного портфеля (комбинация №4). Менеджеры опционных фондов, опционные маркет-мэйкеры и игроки волатильностью — все они вовлечены в процесс синтеза опционных портфелей, осуществляемого через сделки по акциям.
Примечания
1. Triple witching day (ориг.). В настоящий момент времени это уже кануло в историю, потому что главные опционные серии опционов на фондовые фьючерсы завершаются ранее на один день, чем опционы, торгуемые на акции.
2. Barings Bank.